Le calcul de Monsieur Kaprekar

Identification

Rallye: 20.II.19 ; catégorie: 10 ; domaines: FN, AL, OPN
Familles:

• ADD - Rechercher une somme ou une différence de nombres
• ALG - Utiliser un algorithme
• DEM - Effectuer une démonstration

Remarque et suggestion

Résumé

Un nombre de trois chiffres tous différents étant donné, appliquer une procédure de calcul indiquée, constater qu’elle donne toujours le même résultat, le déterminer et justifier son unicité.

Enoncé

Tâche de résolution et savoirs mobilisés

- Comprendre que si M. Kaprekar peut connaître par avance le résultat, c’est que celui-ci est unique, facile à déterminer avec un seul exemple.

- Désigner par K(n) (ou une autre notation) le résultat pour le nombre n du calcul de M. Kaprecar et donner un exemple : K(819) = 981 – 189 = 792.

- Appliquer encore quatre fois ce calcul aux résultats successifs : K(792) = 693 ; K(693) = 594 ; K(594) = 495 ; K(495) = 495 et conclure que le nombre de M. Kaprekar est 495.

- Pour répondre à la deuxième question, après avoir appliqué K sur quelques exemples, remarquer que les résultats successifs ont 9 pour chiffre central, sont divisibles par 9, la somme des chiffres des centaines et des unités valant toujours 9.

- Remarquer que les résultats suivants sont des nombres qui ont un 9 au centre et que les deux autres chiffres sont suivant les cas 1-8 ; 2-7 : 3-6 ; 4-5. Se rendre compte que, selon le calcul de M. Kaprekar, chaque nombre de la forme x9y donne le même résultat que y9x et qu’il suffit donc d'effectuer les calculs pour ces quatre cas.

- Procéder systématiquement en commençant par exemple par 198, trouver 792, puis 693, puis encore 594 et enfin 495. Appliquer cette procédure à 297, à 396 et à 495 et conclure que 495 est le nombre de M. Kaprekar.

Ou bien, en désignant par a le plus grand chiffre du nombre n, par b l’intermédiaire et par c le plus petit, écrire formellement K(n) = (100a + 10b + c) – (100c + 10b + a) = 99 (a – c) et en déduire qu’il est divisible par 99.

- Remarquer que a – c ≥ 2 (puisqu’il y a b entre eux et que les 3 chiffres sont différents) et qu’il y a seulement 8 multiples possibles de 99 comme valeurs pour K(n).

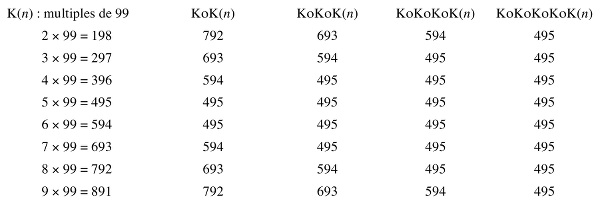
- Calculer ces 8 multiples (multiplier par 100 et soustraire le facteur) et appliquer à chacun 4 fois successivement la fonction K. Dresser le tableau de calcul suivant en remarquant qu’il n’y a que 8 fois à calculer K :

Notions mathématiques

algorithme, opérations arithmétiques, divisibilité par 9, multiple, fonction composée, base dix, soustraction

Résultats

20.II.19

Sur 78 classes ayant participé à la première épreuve du 19e RMT, les points attribués sont les suivants :

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte (495) avec indication claire et précise des régularités, déterminées à partir de deux exemples ou plus et avec explication de la procédure suivie avec le détail des calculs
• 3 points: Le nombre 495 avec une explication peu claire,
  ou la donnée d’un tableau de calculs sans commentaires
• 2 points: Le résultat 495 expliqué par un ou deux exemples traités et l’argument que l’énoncé permet de supposer que le résultat est unique, un seul calcul permet donc de l’obtenir,
  ou bien 495 obtenu après plus de trois essais et l’argument qu’il y a de fortes chances que ce soit ce nombre que M. Kaprekar a écrit
• 1 point: Le résultat 495 sans explication ou avec un ou deux exemples de calcul
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Les procédures observées consistent à appliquer à différents exemples le calcul de Kaprekar et ensuite à observer des régularités dans les résultats obtenus. Dans quelques copies, l'analyse est faite en considérant tous les cas possibles et a par conséquent la valeur d'une vraie démonstration.

Voici quelques observations relevées dans certaines copies :

• le chiffre central (des dizaines) est 9,
• la somme des chiffres est 18, ou la somme des deux chiffres extrêmes (centaines et unités) est 9,
• à partir de la deuxième soustraction, le chiffre des unités augmente et celui des centaines diminue d’une unité,
• les différences entre un nombre et le suivant sont des multiples de 99,
• à partir de la seconde soustraction, les différences diminuent toujours de 99.

Parmi les obstacles que les élèves peuvent rencontrer, on peut signaler la confusion entre chiffre et nombre.

Certains élèves s'arrêtent après la première soustraction, et ne respectent pas la consigne de répéter l’algorithme 5 fois.

D’autres utilisent dans leurs exemples des chiffres égaux.

Enfin, on trouve la déduction de la propriété générale à partir seulement de quelques exemples.

Exploitations didactiques

Il s'agit d'un problème dans lequel le résultat (le nombre de Kaprekar : 495) est facilement réalisable en appliquant la procédure indiquée dans l’énoncé du problème, mais dans lequel il est difficile d’expliquer pourquoi on arrive toujours au même nombre. Une approche observée consiste à introduire des variables a, b, c pour noter les chiffres du nombre initial. Il peut être représenté sous la forme polynomiale 100a + 10b + c ou simplement par abc.

Dans le premier cas, il est plus facile de démontrer une des régularités observées, c’est-à-dire que les différences possibles sont toutes multiples de 99 : (100a + 10b + c) – (100c + 10b + a) = 99 (a – c).

Dans le second cas, en écrivant en colonne la soustraction (abc) – (cba), comme c est plus petit que a, par emprunt d’une dizaine, on voit que le chiffre des dizaines est 9. Puis, la soustraction devient (9de) – (ed9) et à nouveau on peut conclure que le chiffre des unités augmente de 1 et celui des centaines diminue de 1. Cette analyse approfondie de l’algorithme de la soustraction conduit finalement à la démonstration que le nombre de Kaprekar est 495.

Le nombre cherché peut être obtenu par des essais organisés, après observations de régularités, sans que son unicité soit prouvée. Le problème est donc accessible dès le niveau 8. Cependant son intérêt didactique est de mettre en évidence l’utilité de la décomposition du nombre choisi en base 10. Ce système de numération apparaît alors comme outil de résolution de ce type de problèmes jouant sur la place des chiffres dans un nombre.

Bibliographie

Groupe fonction (2014). Le calcul de monsieur Kaprekar. Etude ARMT (http://www.projet-ermitage.org/ARMT/doc/etude-fn9-fr.pdf)

L’encyclopédie en ligne Wikipédia donne accès à de nombreuses études sur le sujet : http://fr.wikipedia.org/wiki/Algorithme_de_Kaprekar

Dattatreya Ramachandra Kaprekar (1905 - 1988) est un mathématicien indien connu pour ses recherches sur les nombres. On lui doit la notion de nombre de Kaprekar ainsi que l'algorithme de Kaprekar. Boudé par ses contemporains, ses travaux seraient passés inaperçus s'il n'avaient pas été relayés par Martin Gardner, spécialiste des énigmes mathématiques (Wikipedia).

(c) ARMT, 2012-2024