
Banca di problemi del RMT
fn9-it
 |
Banca di problemi del RMTfn9-it |
|
Dato un numero di tre cifre tutte distinte, applicare la procedura indicata, verificare che con essa si ottiene sempre lo stesso risultato, determinarlo e giustificarne l’unicità.

- Comprendere che se Kaprekar può conoscere in anticipo il risultato, questo è unico, facile da determinare con un solo esempio.
- Indicare con K(n) (o con un’altra notazione) il risultato per il numero n del calcolo di Kaprekar e dare un esempio: K(819) = 981 – 189 = 792.
- Applicare ancora quattro volte questo calcolo ai risultati successivi : K(792) = 693 ; K(693) = 594 ; K(594) = 495 ; K(495) = 495 e concludere che il numero di Kaprekar è 495.
- Per rispondere alla seconda richiesta, dopo aver applicato K su qualche esempio, osservare che i risultati successivi hanno 9 come cifra centrale, sono divisibili per 9 e la somma delle cifre delle centinaia e delle unità vale sempre 9.
- Considerare che i risultati successivi sono numeri che hanno 9 al centro e le due altre cifre sono di volta in volta 1-8; 2-7: 3-6; 4-5. Rendersi conto che, per come è definito il calcolo di Kaprekar, ogni coppia x9y porta allo stesso risultato di y9x e che quindi basta effettuare i calcoli per quattro casi.
- Procedere in modo sistematico iniziando per esempio da 198, trovare quindi 792 poi 693, poi ancora 594 ed infine 495. Applicare il procedimento a 297, 396 e 495 e concludere che 495 è il numero di Kaprekar.
Oppure, indicando con a la più grande cifra del numero n, con b quella intermedia e con c la più piccola, scrivere formalmente K(n) = (100a + 10b + c) – (100c + 10b + a) = 99 (a – c) e dedurne che è divisibile per 99.
- Osservare che a – c ≥ 2 (poiché c’è b tra essi e le 3 cifre sono differenti) e che ci sono solo 8 multipli possibili di 99 come valori per K(n).
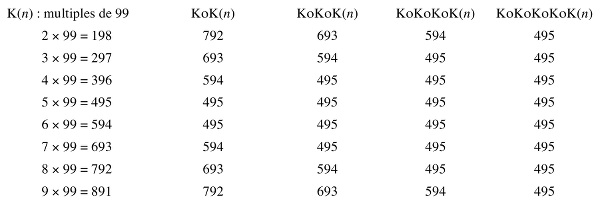
- Calcolare questi 8 multipli (moltiplicare per 100 e sottrarre il fattore) e applicare a ciascun 4 volte successivamente la funzione K. Compilare la tabella di calcolo seguente osservando che occorre calcolare K per 8 volte:
algoritmo, aritmetica, divisibilità per 9, multiplo, funzione composta
Su 78 classi partecipanti alla seconda prova del 19° RMT, sono stati attribuiti i seguenti punteggi :
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 10 | 15 (19%) | 29 (37%) | 13 (17%) | 11 (14%) | 10 (13%) | 78 | 1.64 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Le procedure osservate consistono nell’applicare a diversi esempi il calcolo di Kaprekar e osservare delle regolarità nei risultati ottenuti. In qualche elaborato l’analisi è fatta con la consapevolezza di considerare tutti i casi possibili e quindi ha il valore di una vera e propria dimostrazione.
Alcune osservazioni riscontrate negli elaborati delle classi:
Fra gli ostacoli che gli allievi possono incontrare segnaliamo anzitutto la confusione fra cifra e numero.
Alcuni allievi si fermano alla prima sottrazione, non rispettando la consegna di ripetere l’algoritmo 5 volte.
Altri utilizzano nei loro esempi cifre uguali.
Infine abbiamo trovato la deduzione della proprietà generale a partire soltanto da pochi (2/3) esempi.
Si tratta di un problema nel quale il risultato (il numero di Kaprekar: 495) è facilmente ottenibile applicando la procedura indicata nell’enunciato del problema ma nel quale è difficile spiegare perché si arriva sempre allo stesso numero.
Un approccio osservato consiste nell’introduzione di variabili a, b, c per indicare le cifre del numero iniziale. Esso può essere rappresentato in forma polinomiale 100a + 10b + c oppure semplicemente con la stringa abc.
Nel primo caso è più facile dimostrare una delle regolarità osservate e cioè che le possibili differenze sono tutte multipli di 99: (100a + 10b + c) – (100c + 10b + a) = 99 (a – c).
Nel secondo caso, scrivendo in colonna la sottrazione (abc)-(cba) si giustifica, mediante il meccanismo del “prestito” (c è minore di a), che la cifra delle decine è 9. Successivamente, la sottrazione diventa (9de)-(ed9) e, ancora col meccanismo del “prestito” si può concludere che la cifra delle unità aumenta di 1 e quella delle centinaia diminusce di 1. Questa analisi approfondita dell’algoritmo della sottrazione conduce alla fine alla dimostrazione che il numero di Kaprekar è 495.
l numero cercato può essere ottenuto mediante tentativi organizzati, dopo osservazioni di regolarità, senza che sia provata la sua unicità. Il problema è, dunque, accessibile già dal livello 8. Comunque il suo interesse didattico è quello di mettere in evidenza l'utilità della scomposizione del numero scelto in base 10. Questo sistema di numerazione si rivela allora uno strumento di risoluzione di questo tipo di problemi che giocano sulla posizione delle cifre in un numero.
Grupo funzione (2014). Il calcolo di Kaprekar. Studio ARMT (http://www.projet-ermitage.org/ARMT/doc/studio-fn9-it.pdf)
L'enciclopedia in rete Wikipedia dà accesso a numerosi studi sul soggetto: http://fr.wikipedia.org/wiki/Algorithme_de_Kaprekar
Dattatreya Ramachandra Kaprekar (1905 - 1988) era un matematico indiano noto per le sue ricerche sui numeri. A lui si devono la nozione di numero di Kaprekar e di algoritmo di Kaprekar. Ignorato dai suoi contemporanei, i suoi lavori sarebbero passati inosservati se non fossero stati pubblicizzati da Martin Gardner, esperto di enigmi matematici (Wikipedia).
(c) ARMT, 2012-2024