
Banca di problemi del RMT
gm25-it
 |
Banca di problemi del RMTgm25-it |
|
Confrontare il livello di liquido in due barattoli cilindrici uguali conoscendo il ritmo di riempimento di ciascuno dei due recipienti.
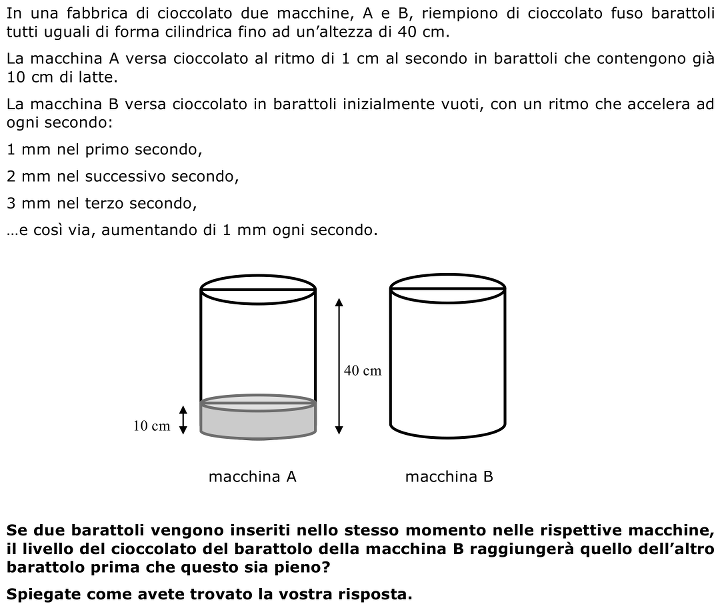
Analisi a priori:
- Calcolare il tempo che occorre affinché il livello del barattolo riempito dalla macchina A raggiunga il livello di 40 cm: resta quindi da riempire un’altezza di 30 cm e poiché si riempie di 1 cm al secondo occorrono 30 secondi per finire di riempire il barattolo A.
- Calcolare l’altezza che raggiunge il cioccolato nel barattolo della macchina B dopo 30 secondi: (1 + 2 + 3 + 4 +…+ 30) mm, eseguendo la somma a mano oppure riconoscendo che è uguale a (31 × 30) / 2 = 465 mm = 46,5 cm.
- Concludere che in 30 secondi il cioccolato del barattolo della macchina B sorpasserebbe il livello di quello della macchina A e che quindi raggiunge il livello dell’altro barattolo prima che questo sia pieno.
Oppure:
Calcolare le altezze raggiunte dal cioccolato nei due barattoli al passare del tempo, eventualmente aiutandosi con una tabella di questo tipo:

- Concludere che il livello del cioccolato del barattolo della macchina B raggiungerà quello della macchina A dopo circa 27 secondi, cioè prima che quest’ultimo sia completamente pieno.
Oppure:
- Per via algebrica e/o grafica determinare sia il momento in cui il livello di 400 mm è raggiunto nel barattolo della macchina B, sia il momento in cui i due barattoli sono allo stesso livello: bisogna allora, nel primo caso la (durata: t, in secondi) trovare la formula 1 + 2 + 3 + ... + t = (t+1) × t/2 e risolvere l’equazione (t+1) × t/2 = 400, la cui la soluzione $\frac{-1 \pm \sqrt{1+3200}}{2} \approx 27.8$.
- Concludere che il livello del cioccolato nel barattolo della macchina B arriverà all’altezza 40 cm (400 mm) prima di quello della macchina A (in 30 secondi); oppure, nel secondo caso, esprimere le due funzioni f(t) = 10 + t ; g(t) = (t+1) × t/20 e risolvere l’equazione f(t) = g(t) ; 10 + t = (t+1) × t/20 di cui la radice positiva è uguale a 26,53 s.
volume, cilindro, portata, velocità
Punti attribuiti, su 402 classi di 8 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 9 | 39 (19%) | 29 (14%) | 30 (15%) | 44 (21%) | 64 (31%) | 206 | 2.32 |
| Cat 10 | 29 (15%) | 28 (14%) | 23 (12%) | 47 (24%) | 69 (35%) | 196 | 2.51 |
| Totale | 68 (17%) | 57 (14%) | 53 (13%) | 91 (23%) | 133 (33%) | 402 | 2.41 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
La maggior parte delle soluzioni corrette si basa su un ragionamento aritmetico del tipo seguente: /
- Calcolo del tempo di riempimento del barattolo A: 30 secondi
- Per il barattolo B: esecuzione della somma 1+2+3+… fino a superare il valore 400 (400 mm= 40 cm)
- Osservazione che al 28° secondo il liquido raggiunge l’altezza 406 mm che garantisce il totale riempimento del barattolo B, prima che A sia completamente pieno
Oppure:
- Calcolo del tempo di riempimento del barattolo A: 30 secondi
- Per il barattolo B: esecuzione della somma 1+2+3+… con 30 addendi, che dà il valore 465 (465 mm= 46,5 cm)
- Osservazione che al 30° secondo, quando il barattolo A è pieno, il barattolo B è sicuramente pieno perché l’altezza del liquido sarebbe 46,5 cm
In diversi elaborati (26% degli elaborati con punteggio 4) si trovano tabelle con l’altezza del cioccolato nel barattolo B, o in entrambi i barattoli, calcolate agli istanti di tempo 1, 2, 3, …30 o solo in alcuni di questi istanti. Queste tabelle permettono di osservare che poco prima del 27° secondo il livello del barattolo B supera quello del barattolo A e/o che poco prima del 28° secondo il barattolo B sarà completamente pieno.
tempo alt. alt. (s) A (mm) B (mm) 0 100 0 1 110 1 2 120 3 3 130 6 4 140 10 5 150 15 6 160 21 … … … 24 340 300 25 350 325 26 360 351 27 370 378 28 380 406 29 390 435 30 400 465
In qualche elaborato è stata utilizzata la formula n*(n+1)/2 con n=30 oppure n=28. In alcuni casi (2 sui 45 elaborati di cat. 9 della sezione PR) la formula è stata applicata con il valore n=27,79 (trovato, si dice, per tentativi) per verificare che questo sia il tempo di riempimento del barattolo B (27,79*28,79/2=400). In un caso (sui 48 elaborati di cat.10 della sezione PR) è stata risolta l’equazione n*(n+1)/2=40 per trovare il tempo di riempimento del barattolo B.
In numerosi elaborati di cat.10 il processo di riempimento dei barattoli A e B viene assimilato a due moti che avvengono rispettivamente con velocità costante (A) e accelerazione costante (B). Si tratta di una strategia molto diffusa in cat. 10 e non prevista dall’analisi a priori, che a causa di un errore nella scrittura della legge oraria, la rende meno efficace di quella della rappresentazione in tabella.
Infatti la legge oraria di A viene scritta correttamente: h = 10 + t (h in cm, t in s), mentre per B viene individuata correttamente l’accelerazione (1 mm/s$^2$) ma non la velocità iniziale, che viene erroneamente interpretata come nulla. Viene quindi scritta la legge oraria h = 1/2t$^2$2 (h in mm, t in s), da cui viene dedotto il tempo di riempimento del barattolo B di circa 28 secondi (28,28), valore che si discosta di poco da quello corretto (27,79).
Per tutte le strategie, gli errori riscontrati sono sempre relativi al processo di riempimento del barattolo B. In molti casi la mancanza di motivazioni non permette di risalire alla causa delle risposte errate; quando possibile, sono stati identificati:
- Errato utilizzo della proporzionalità (per esempio calcolato il tempo di riempimento del barattolo B nei primi 4 secondi (10 mm) e dedotto il tempo di riempimento totale x dalla proporzione 4 sec:10mm=x:400mm)
- Errori di calcolo nella somma 1+2+3+…. o nei valori riportati nelle tabelle
- Errori con le unità di misura nelle conversioni fra mm e cm (poco rilevanti in questo problema)
- Errore, già citato, nella scrittura della legge oraria h=1/2 t$^2$ invece di h=1/2 t+1/2 t$^2$
- Errori nell’interpretazione dei dati della tabella: in un caso si conclude che il livello non sarà mai lo stesso nei due barattoli perché si considerano solo istanti di tempo interi
In generale in questo problema la strategia più “elementare” di seguire il processo “passo a passo”, calcolando il livello di riempimento del barattolo B ad ogni secondo, è risultata più efficace della strategia più “raffinata” di sintetizzare il fenomeno in una relazione fra le variabili tempo ed altezza. In altre parole questa situazione si presta meglio ad essere affrontata mediante una successione che non attraverso una funzione di variabile reale.
La strategia “passo a passo” con l’eventuale rappresentazione in tabella mostra già la consapevolezza di grandezze variabili collegate fra loro. Può essere il punto di partenza per una discussione in classe che stimoli la ricerca di una legge funzionale per i due processi di crescita (lineare per il processo A e di secondo grado per B). Contemporaneamente o successivamente potrà nascere l’esigenza di una rappresentazione grafica delle due funzioni (retta per A e parabola per B), trasferendo così definitamente l’attenzione dal discreto al continuo e dando una significativa interpretazione al punto di intersezione delle due curve.
La ricerca della legge a partire dalle coppie di valori numerici dovrebbe portare anche ad un chiarimento sulla presenza di una velocità iniziale non nulla nel processo B, modellizzato con un moto rettilineo uniformemente accelerato. L’errore di assumere come nulla tale velocità (nel quale noi stessi “esperti” in prima battuta siamo caduti) rimanda ad un importante nodo concettuale, ovvero ancora la distinzione fra processi discreti e processi continui o, dal punto di vista fisico, tra valori medi e valori istantanei.
(c) ARMT, 2018-2025