Les cinq rectangles (II)

Identification

Rallye: 27.II.17 ; catégories: 8, 9, 10 ; domaines: GP, GM
Familles:

• LA - Utiliser des mesures de longueurs et aires
• RD - Rechercher ou utiliser des dimensions
• RD/AP - Déterminer des aires et/ou périmètres

Remarque et suggestion

Résumé

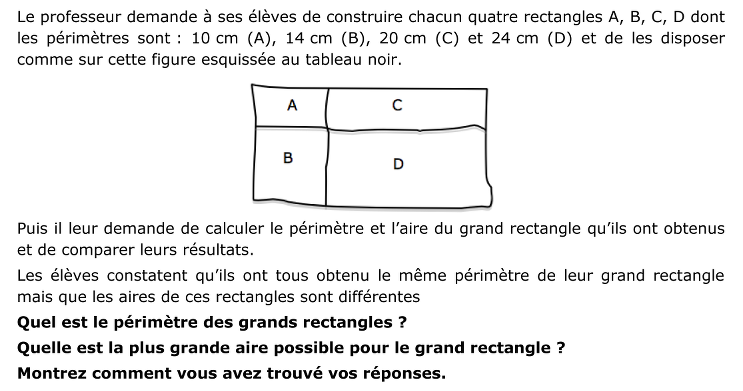
Former des rectangles composés chacun de quatre rectangles de périmètres 10, 14, 20 et 24 cm, et déterminer leur périmètre et trouver lequel de ces rectangles a une aire maximale.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse a priori:

- Observer la figure et comprendre pourquoi il y a différents rectangles de 10 14, 20 et 24 cm de périmètre (ils peuvent être plus ou moins « allongés », et même carrés.

- Comprendre que si on choisit la longueur d’un côté du rectangle de 10 cm de périmètre, la longueur de l’autre côté est déterminée et peut se calculer par la relation : le périmètre est la somme des quatre longueurs des côtés, deux largeurs et deux longueurs. Par exemple :

• - si l’on choisit 1 cm pour la largeur, la longueur sera 4 cm (10 = 2 × 1 + 2 × 4)
• - si l’on choisit 1,5 cm pour la largeur, la longueur sera 3,5 cm (10 = 2 × 1,5 + 2 × 3,5)

- Constater que toutes les autres dimensions des trois autres petits rectangles et du grand sont aussi déterminées par la valeur choisie pour une des dimensions du premier petit rectangle.

- Pour répondre aux deux questions sur le périmètre et l’aire les calculs peuvent par exemple être regroupés sous cette forme ordonnée à partir d’une dimension du premier rectangle, de 10 cm :

et constater la constance du périmètre et l’augmentation puis la diminution « symétriques » de l’aire autour de 72 pour les valeurs de 3 et de 3,5, pour comprendre qu’il est nécessaire d’insérer une nouvelle valeur 3,25 :

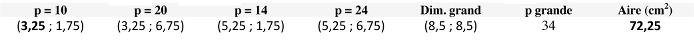
Constater alors, vu la « symétrie » des variations (augmentations suivies de diminutions correspondantes) que le plus grand rectangle a une aire de 72,25 cm2.

- On peut aussi arriver à cette conclusion en sachant que, parmi tous les rectangles de 34 cm de périmètre, c’est le carré de 8,5 cm de côté dont l’aire est la plus grande.

Ou :

résoudre le problème par la recherche du maximum de la fonction A = x (17 – x) où la variable est le premier côté d’un rectangle de 34 cm de périmètre.

Notions mathématiques

carré, rectangle, périmètre, longueur, côté, division, addition

Résultats

27.II.17

Points attribués sur 1211 classes de 18 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponses correctes et complètes (tous les périmètres mesurent 34 cm et l’aire maximale est 72,25 cm2), avec les détails de tous les calculs.
• 3 points: Réponses correctes et complètes avec explications partielles ou peu claires
  ou réponse correcte pour les périmètre et une aire de 72 cm2 avec explications claires (le maximum n’ayant pas été envisagé lorsque le grand rectangle devient un carré de côté 8,5,)
• 2 points: Réponses correctes et complètes sans explications
  ou réponse correcte pour les périmètre et une aire de 72 cm2 avec explications partielles et peu claires
  ou réponse erronée due à une seule erreur de calcul, avec des explications claires
• 1 point: Début de recherche cohérent
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Première analyse de (101 copies de FC)

Une majorité des groupes a trouvé le périmètre 34 à partir d’un seul essai de valeurs des côtés du rectangle de 10 cm de périmètre : en général 2 et 3. Dans un cas l’aire du grand rectangle est 66, dans l’autre cas 72 et c’est la valeur qui a été compris comme la plus grande aire.

Quelques groupes ont vérifié le périmètre 34 à partir de deux essais : 2 ; 3 et 1 ; 4

Seuls deux copies font état d’essais avec des mesures non entières :3,5 et 1, 5 et 4,5 et 0,5.

Quelques réponses ont conduit à 70 pour l’aire du grand rectangle, à partir de l’essai 4 ;1.

Seuls deux groupes ont perçu la classe des rectangles de périmètre 34 :

- La plus grande aire est 72,2499 cm. Pour trouver, on a, à partir du périmètre, fait des essais avec des longueurs et largeurs les plus rapprochées. Le périmètre étant 34 cm, on a pris comme longueur 8,51 cm et comme largeur 8,49 cm. On les a multipliés et le résultat était 72,2499 cm. On a essayé avec des valeurs plus éloignées et l’aire inférieure à celle de 72,2499. On remarque que, pour ces élèves, le carré (de côté 34/4 ou 8,5) n’appartient pas à la classe des rectangles.

- Comme pour le rectangle A, nous avons divisé le périmètre par 2 pour trouver sa moitié. On sait que la longueur × largeur = aire du rectangle, (34 :2 = 17). Si on prend deux chiffres qui donnent 17 une fois additionnés. par tâtonnements on commence par 2 et 15 (qui font 17) on fait 2× 15 = 30, on essaye d’autres possibilités comme 4 × 13= 52 ; 6× 11= 66, on voit que plus l’écart entre les deux chiffres est faible plus l’aire est grande. On décide de prendre la moitié de 17 (8,5) puisqu’on a pris la moitié de 17, l’écart est nul, on fait 8,5× 8,5 ce qui donne 72,25. La plus grande aire possible de ce rectangle est 72,25 cm².

Il y a de nombreuses incompréhensions de « grand rectangle » de l’énoncé. Pour les adultes il s’agit de la réunion des quatre rectangles A, B, C, D, mais pour certains élèves, il s’agit de D (le plu grand sur la figure) ou des autres rectangles aussi puisque leur aire dépend des valeurs choisies pour les mesures des côtés.

Obstacles. La majorité de 0 pt et 1 pt révèle que le problème présente des obstacles importants. Nous avons vu que la recherche du maximum n’est pas possible si les rectangles de 34 cm de périmètre ne sont pas conçus comme appartenant à un classe d’une infinité de rectangles mais comme un ou deux cas particuliers. Mais si on se limite à la recherche du périmètre du grand rectangle, on constate 25% d’échecs.

Il y a encore des confusions entre aire et périmètre, des difficultés à utiliser les relations d’égalités entre côtés de rectangles contigus et, surtout une conception du périmètre comme somme de longueurs des côtés qui se limitent à ceux dont les mesures sont entières.

(c) ARMT, 2019-2024