Le défi

Identification

Rallye: 11.F.04 ; catégories: 3, 4, 5 ; domaines: GP, GM
Famille:

• RO - Paver une figure de manière optimale

Remarque et suggestion

Résumé

Placer dans une grille de 5 x 5 le plus grand nombre de pièces en forme de L (deux branches perpendiculaires de 1 x 3 avec une extrémité commune).

Enoncé

Tâche de résolution et savoirs mobilisés

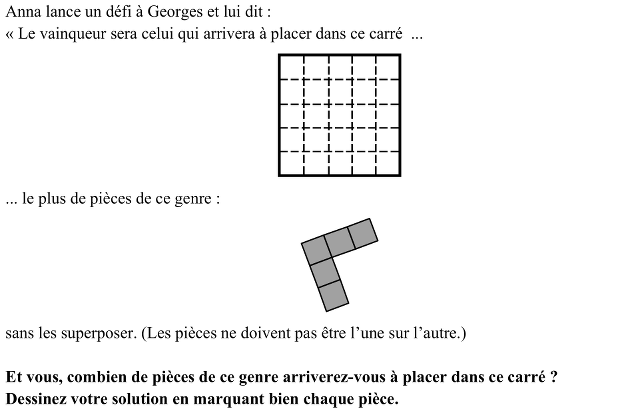
Disposer sur une grille de 5 x 5, et sans qu’elles se superposent, un maximum de pièces identiques en forme de L (deux branches perpendiculaires de 1 x 3 avec une extrémité commune) occupant chacune exactement 5 carrés de la grille.

Savoir reconnaître la pièce dans ses différentes positions : permanence ou invariance de la figure géométrique par des translations ou des rotations (la symétrie axiale ou « retournement n’entre pas en compte vu que la pièce a un axe de symétrie).

Savoir dessiner ou reporter les pièces sur la grille.

Surmonter le conflit provoqué par l’impossibilité de recouvrir la grille entièrement et émettre des hypothèses qui font intervenir le nombre de carrés de la grille et de la pièce (idée d’aire) et la forme de la pièce.

Les savoirs mobilisés sont pour l’essentiel : reconnaître une figure dans différentes positions, prendre en compte la forme des pièces et de la surface à paver pour agencer les pièces de façon à minimiser le nombre de carreaux de la grille qui ne seront pas recouverts

Notions mathématiques

comparaison d'aires, pavage, carré

Résultats

11.F.04

Sur la base des copies de 111 classes finaliste de 13 sections italiennes, suisses et belges.

Selon les critères recopiés de l’analyse a priori du problème :

• 4 points: Solution optimale (4 pièces) avec un dessin précis et claire
• 3 points: Solution optimale (4 pièces) avec un dessin peu précis
• 2 points: Solution avec 3 pièces avec un dessin précis et claire
• 1 point: Réponse "4 pièces" sans dessins ou réponse "5 pièces" avec l'opération 25:5 = 5
• 0 point: Incompréhension du problème: pièces superposées, etc.

Procédures, obstacles et erreurs relevés

Les incompréhensions relevées en catégorie 3 (27%) disparaissent les années suivantes. Globalement, la moitié des élèves arrivent à disposer 3 pièces sur la grille et environ 30 % trouvent la solution optimale.

L’obstacle est ici d’ordre quasi « mécanique », et lié, semble-t-il à la relation entre le nombre, maximum, de pièces et le nombre, minimum, de cases vides : on commence naturellement par placer une pièce dans un angle de manière qu’elle ne laisse aucune case vide entre elle et le bord de la grille ! et cette intuition devient un obstacle majeur puisque la solution optimale avec 4 pièces laisse précisément les quatre cases des angles vides, avec celle du centre.

On ne trouve que de très rares références à l’aire de 25 carrés correspondant à celles de 5 pièces, mais certaines fois des « convictions » que malgré les multiples essais aboutissant à 3 pièces, on devrait tout de même arriver à 4, sachant qu’on ne pourra arriver à 5 en raison de la forme en L.

Exemple d’un groupe qui n’est arrivé qu’à 3 pièces (Cat. 4) : Abbiamo composto molti quadrati che pèro erano con 3 di quelle formine, mentre, secondo noi, nel quadrato ce ne sono 4. / Nous avons complété plusieurs carrés, qui n'avaient que 3 pièces de cette forme, mais selon nous dans le carré il doit y en avoir 4.

Autre exemple, relevé lors d’une expérimentation en classe : Camilla, di quinta elementare dice di aver capito che era la giusta soluzione perché pur avanzando 5 quadretti, cioè l’equivalente di una elle, non era possibile sistemarne altre perché la forma non lo rendeva possibile. / Camille, de cinquième année primaire dit avoir compris qu'elle a la bonne solution parce que, bien u'il reste 5 carrés, c'est-à-dire l'équivalent d'une pièce en L, il n'est pas possible d'en placer d'autres parce que la forme ne le permet pas.

L’unique référence explicite à l’aire, sur les 54 copies de vainqueurs des finales régionales est la suivante, d’une classe de catégorie 5 : Noi pensiamo che il massimo dei pezzi sia quattro perchè l’area del quadrato è di 25 mentre l’area di un pezzo è di 5. Però per completare tutto il quadrato un pezzo bisogneva toglierlo. / Nous pensons que le maximum des pièces est quatre parce que l'aire du carré est 25 et l'aire d'une pièce est 5. Mais pour compléter tout le carré il fallait enlever une pièce.

Exploitations didactiques

Dans sa version actuelle, le problème conduit à un conflit constructif entre l’aire et la forme des figures qui interviennent : carré et pièces en forme de L.

Des expérimentations ont été conduites dans plusieurs classes (voir la rubrique « Pour aller plus loin »). Elles montrent qu’une situation comme Le défi, qui en première lecture ne semble qu’un « petit jeu de placement de pièces », conduit au constat de l’impossibilité de recouvrir entièrement la grille en faisant appel aux différentes isométries possibles et à des explications d’ordre numérique, en nombres de carrés, approche « naturelle » de la mesure d’aires.

Pour aller plus loin

Le problème « Le défi » a été proposé depuis la première année primaire (avec des modalités particulières) et l’analyse a posteriori qui en a été faite donne une image assez claire de son utilisation possible dans la salle de classe comme problème d'apprentissage. Selon l'analyse effectuée par le groupe de travail RMT à Arco (Italie), avec comme support les productions des classes qui ont participé au rallye, ce problème se prête bien à l’approche de la notion d’aire. Il s'agit de comparer des surfaces toutes réalisées avec des carrés identiques.

Le fait qu’il n’est pas possible de recouvrir entièrement la grille et qu’il reste 5 carreaux blancs est très important. La présence de carrés non recouverts peut faire réfléchir les élèves sur le fait que « s’ils existent », ils ne peuvent pas être « mesurés » ou comptabilisés.

L'analyse des productions confirme cette hypothèse. Une copie montre la présence de croix tracées sur chacun des 5 carrés non recouverts.

L'analyse a posteriori a été réalisée à partir des productions des élèves et des discussions qui ont suivi dans chaque classe. Pour connaître le détail des expériences et des observations réalisé, consulter les articles cités dans la bibliographie.

Bibliographie

Bisso C., Grugnetti L. (a cura di): 2006, ‘Approccio al concetto di area con problemi del RMT’, Gruppo di lavoro n° 8, “ellealquadrato”, in R. Battisti, R. Charnay, L. Grugnetti, F. Jaquet (Eds.) RMT : des problèmes à la pratique de la classe/RMT: dai problemi alla didattica quotidiana, Actes des journées d’études sur le Rallye mathématique transalpin, Bourg-en-Bresse 2004, Arco di Trento 2005, ARMT, IUFM de Lyon-Centre de Bourg-en-Bresse, IPRASE Trentino , 268-276.

Bisso C. Grugnetti L.: ‘Il ruolo dei problemi del RMT nella costruzione del concetto di area’, in L. Grugnetti, F. Jaquet, D. Medici, M. G. Rinaldi, I problemi del RMT nella didattica quotidiana/ les problèmes du RMT dans la pratique de la classe, Parma 2006, Sezione ARMT di Parma, ARMT.

Bisso C., Grugnetti L. (2006), « La costruzione del concetto di area con problemi del RMT », Gruppo di lavoro n° 6, “ellealquadrato”, in R. Battisti, R. Charnay, L. Grugnetti, F. Jaquet, D. Medici, M.-G. Rinaldi (Eds.) I problemi come supporto per l’apprendimento : il ruolo del RMT / Les problèmes au service de l’apprentissage : le rôle du RMT Parma 2006, ARMT, Dipartimento di Matematica dell’Università di Parma, Sezione ARMT di Parma, 169-187.

Douady R., Perrin-Glorian M.-J. (1989), « un processus d’apprentissage du concept d’aie de surfaces planes », Educational studies in mathematics, 20, 387-424

ERMEL (2006), Apprentissages géométriques et résolution de problèmes au cycle 3. Hatier Ed, Paris

Jaquet F. (2000), « Il conflitto aera-perimetro », L’educazione matematica, Ed CRSEM, VI, 21, 2, (prima parte : n.2, 66-77, seconda parte : n.3, 126-143)

Rouche N. (1992), Le sens de la mesure, Formation Didier Hatier

(c) ARMT, 2003-2024