
Banca di problemi del RMT
gp1-it
 |
Banca di problemi del RMTgp1-it |
|
Sistemare su una griglia 5 x 5 il maggior numero di pezzi in forma di L (due strisce perpendicolari di 1 x 3 con un’estremità comune)
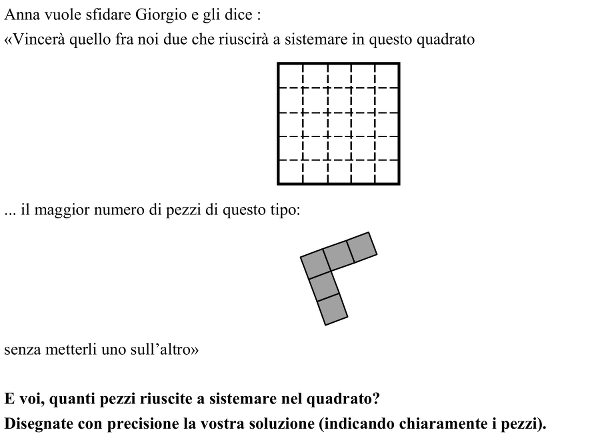
Questo problema richiede di disporre il numero massimo di pezzi uguali a forma di L (due “bande” perpendicolari di 1 x 3 con una estremità comune) su una griglia 5 x 5, che occupano ciascuno 5 quadretti della griglia, senza che si sovrappongano.
Si tratta di cominciare con il ritaglio o il disegno di alcuni pezzi alla ricerca di un modo ottimale, con pezzi ruotati o spostati (traslazione).
E’ pertanto necessario saper riconoscere i pezzi nelle diverse posizioni cosa che richiede di rendersi conto che i pezzi in gioco (o in generale una figura geometrica) nel ruotare o nelle spostarsi rimangono invariati nella forma e nella grandezza (in termini formali: la permanenza o invarianza della figura geometrica per traslazioni o rotazioni -la simmetria assiale o “ribaltamento” non entra in gioco visto che il pezzo ha un asse di simmetria).
Poiché non si può ricoprire tutto il quadrato bisogna affrontare il conflitto provocato dall’impossibilità di ricoprire interamente la griglia ed emettere delle ipotesi che fanno intervenire il numero di quadretti della griglia e il pezzo a forma di L (idea di area) e la forma del pezzo.
Si tratta di un confronto fra “oggetti” della stessa specie: in questo caso quadretti che induce l’idea di “unità comune”. Importanza della forma.
In sostanza i saperi mobilizzati sono: riconoscere i pezzi nelle diverse posizioni e prendere in conto la forma dei pezzi e della superficie da pavimentare per sistemare i pezzi in modo da minimizzare il numero dei quadrati della griglia che non saranno ricoperti
confronto aree, pavimentazione, quadrati
Punteggi attribuiti su 111 elaborati di classi finaliste di 13 sezioni italiane, svizzere e belghe,
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 3 | 27 (27%) | 6 (6%) | 42 (42%) | 3 (3%) | 22 (22%) | 100 | 1.87 |
| Cat 4 | 3 (3%) | 14 (14%) | 44 (44%) | 6 (6%) | 33 (33%) | 100 | 2.52 |
| Cat 5 | 8 (8%) | 8 (8%) | 56 (55%) | 8 (8%) | 21 (21%) | 101 | 2.26 |
| Totale | 38 (13%) | 28 (9%) | 142 (47%) | 17 (6%) | 76 (25%) | 301 | 2.22 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Le incomprensioni rilevate nella categoria 3 (27%) spariscono nelle categorie successive. Globalmente la metà degli allievi riesce a disporre 3 pezzi sulla griglia e circa il 30 % trova la soluzione ottimale.
L’ostacolo è qui quasi di ordine “meccanico” e legato, sembrerebbe, alla relazione tra il numero, massimo, dei pezzi e il numero, minimo, di caselle vuote: si comincia ovviamente col sistemare un pezzo in un angolo in modo che esso non lasci alcuna casella vuota tra se stesso e il bordo della griglia! E questa intuizione diventa un ostacolo importante perché la soluzione ottimale con 4 pezzi lascia proprio le quattro caselle agli angoli, vuote, insieme a quella centrale.
Sono molto rari i riferimenti all’area di 25 quadretti corrispondente a quella dei 5 pezzi, ma certe volte si trovano delle “convinzioni” che malgrado diversi tentativi portano a 3 pezzi, mentre bisognerebbe arrivare a 4, sapendo che non si potrà arrivare a 5 a causa della forma ad L.
Esempio di un gruppo che è arrivato a 3 pezzi (Cat. 4): Abbiamo composto molti quadrati che però erano con 3 di quelle formine, mentre, secondo noi, nel quadrato ce ne sono 4.
Un altro esempio che proviene da una sperimentazione in classe: Camilla, di quinta elementare dice: di aver capito che era la giusta soluzione perché pur avanzando 5 quadretti, cioè l’equivalente di una elle, non era possibile sistemarne altre perché la forma non lo rendeva possibile.
L’unico riferimento esplicito all’area, sui 54 elaborati dei vincitori delle finali regionali è la seguente, di una classe di categoria : Noi pensiamo che il massimo dei pezzi sia quattro perchè l’area del quadrato è di 25 mentre l’area di un pezzo è di 5. Però per completare tutto il quadrato un pezzo bisognava toglierlo.
Nella sua attuale versione il problema provoca un costruttivo conflitto fra la quadrettatura del quadrato grande e la forma ad L dei pezzi.
Sono state condotte diverse sperimentazioni in classe, descritte nei complementi.
Esse mostrano chiaramente come La Sfida, che in prima lettura sembra solo “un piccolo gioco di sistemazione di pezzi”, evolve verso una constatazione di impossibilità di ricoprire tutto facendo appello a tutte le isometrie possibili, poi può portare con profitto a spiegazioni di ordine numerico, in numero di quadretti, come approccio veramente naturale a delle “misure” di area.
Il problema “La sfida” è stato proposto a partire dalla prima primaria (in questo caso con modalità particolari), e la sua analisi a posteriori offre un quadro piuttosto chiaro della sua utilizzazione in classe come “problema di apprendimento”.
Secondo l’analisi condotta nell’ambito del gruppo di lavoro ad Arco, con il supporto anche di elaborati di classi che avevano partecipato alla gara, questo problema si presta ad essere usato nelle classi nell’ottica di un avvio alla costruzione dell’idea di area.
Si tratta di fare un confronto fra “oggetti” della stessa specie: in questo caso quadretti.
Il gruppo ritiene molto importante la presenza, nella soluzione, di 5 quadretti bianchi. Non è possibile, infatti, ricoprire tutto il quadrato. Quei quadretti bianchi possono far riflettere gli alunni sul fatto che “esiste” anche ciò che non si ricopre o che non si può misurare e contare. L’analisi degli elaborati della gara conferma questa ipotesi. Uno degli elaborati mostra delle x tracciate su ognuno dei 5 quadretti non ricoperti.”
L’analisi a posteriori è stata effettuata sia sulla base degli elaborati dei gruppi di allievi, sia sui resoconti della discussione sviluppata in ciascuna classe.
Per i dettagli delle sperimentazioni e delle osservazioni che ne sono scaturite si rimanda agli articoli citati in bibliografia.
Bisso, C., Grugnetti, L. (a cura di): 2006, ‘Approccio al concetto di area con problemi del RMT’, Gruppo di lavoro n° 8, “ellealquadrato”, in R. Battisti, R. Charnay, L. Grugnetti, F. Jaquet (Eds.) RMT : des problèmes à la pratique de la classe/RMT: dai problemi alla didattica quotidiana, Actes des journées d’études sur le Rallye mathématique transalpin, Bourg-en-Bresse 2004, Arco di Trento 2005, ARMT, IUFM de Lyon-Centre de Bourg-en-Bresse, IPRASE Trentino , 268-276.
Bisso, C., Grugnetti, L.: 2007, ‘Il ruolo dei problemi del RMT nella costruzione del concetto di area’, in L. Grugnetti, F. Jaquet, D. Medici, M. G. Rinaldi, I problemi del RMT nella didattica quotidian a/ les problèmes du RMT dans la pratique de la classe, Parma 2006, Sezione ARMT di Parma, ARMT, 25-36.
(c) ARMT, 2003-2024