
Banca di problemi del RMT
gp113-it
 |
Banca di problemi del RMTgp113-it |
|
Trovare tutti i poligoni che è possibile ottenere unendo, lungo i lati della stessa lunghezza, i due poligoni ottenuti a partire da una divisione di un quadrato in due parti.

- Comprendere che le figure da disegnare sono sempre ottenute dalle stesse due parti del quadrato iniziale, posizionate in modo diverso (è permesso anche ribaltarne una o entrambe) e affiancate in modo da avere un solo lato in comune.
- Analizzare le due parti, trapezio rettangolo e pentagono, in cui è scomposto il quadrato ed individuare relazioni tra i lati delle due figure: la base minore, l’altezza del trapezio e i due lati minori del pentagono sono congruenti; la base maggiore del trapezio e i due lati maggiori del pentagono sono congruenti; il lato obliquo del trapezio e il lato obliquo del pentagono sono congruenti.
- Immaginare di disporre i due pezzi del quadrato secondo le regole indicate e provare a disegnare le figure ottenute su un foglio quadrettato. L’individuazione delle figure può essere facilitata ritagliando un modello del trapezio rettangolo e uno del pentagono e assemblandoli poi in modo che i due modelli abbiano in comune esattamente un lato.
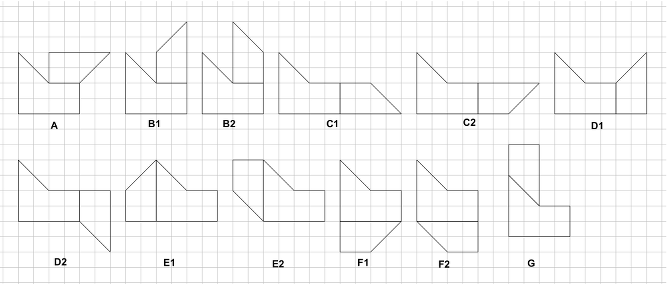
- Procedere in modo non organizzato (in tal caso è probabile che non si trovino tutte le figure), oppure in modo sistematico. Nel secondo caso, considerare, ad esempio, il pezzo a forma di pentagono, scegliere un lato e affiancargli il trapezio rettangolo in modo che coincidano il lato del pentagono e quello, o uno di quelli, della stessa lunghezza nel trapezio. Rendersi conto che, provando a ripetere la stessa operazione dopo aver ribaltato il trapezio rettangolo, solo in alcuni casi si ottiene una seconda figura che non è congruente alla prima (cfr. figure B1 e B2; C1 e C2; D1 e D2; E1 e E2; F1 e F2) mentre negli altri casi, è impossibile costruire una seconda figura (cfr. figure A,G).
- Un compito piuttosto delicato è quello di controllare che le figure ottenute siano tutte non congruenti tra loro. Un metodo efficace per verificarlo sperimentalmente è, per esempio, quello di usare un foglio di carta sottile, riprodurvi una delle due figure e controllare se tale riproduzione, dopo aver ribaltato il foglio, si sovrappone perfettamente o no all’altra figura. (Per questa via si può arrivare ad osservare che figure congruenti sono sempre ottenute una dall’altra ribaltando entrambi i pezzi che le compongono)
- Concludere che le figure cercate (distinte dal quadrato e non congruenti tra loro) sono le 12 riprodotte qui sotto.
Punteggi attribuiti su 229 classi di 17 sezioni:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 6 | 24 (38%) | 17 (27%) | 13 (21%) | 5 (8%) | 4 (6%) | 63 | 1.17 |
| Cat 7 | 13 (21%) | 9 (14%) | 15 (24%) | 16 (25%) | 10 (16%) | 63 | 2.02 |
| Cat 8 | 11 (20%) | 11 (20%) | 10 (19%) | 7 (13%) | 15 (28%) | 54 | 2.07 |
| Cat 9 | 4 (14%) | 5 (18%) | 4 (14%) | 4 (14%) | 11 (39%) | 28 | 2.46 |
| Cat 10 | 1 (5%) | 4 (19%) | 1 (5%) | 5 (24%) | 10 (48%) | 21 | 2.9 |
| Totale | 53 (23%) | 46 (20%) | 43 (19%) | 37 (16%) | 50 (22%) | 229 | 1.93 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
(c) ARMT, 2016-2024