
Banque de problèmes du RMT
gp120-fr
 |
Banque de problèmes du RMTgp120-fr |
|
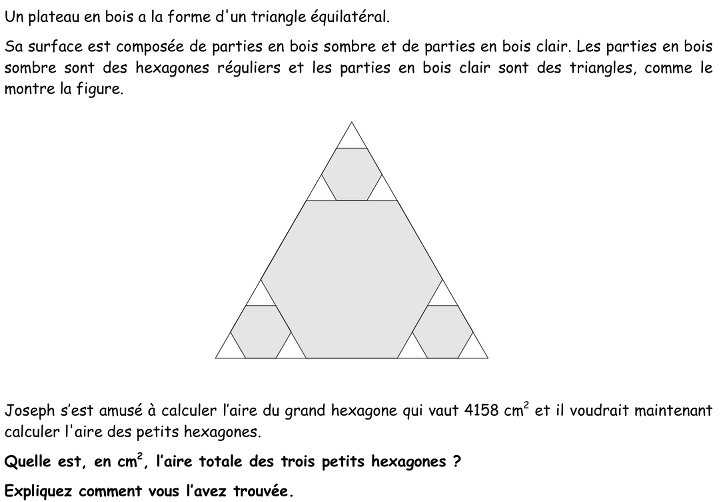
Calculer l’aire de trois hexagones réguliers isométriques construits sur trois côtés d’un hexagone régulier dont l’aire est 4158 cm2, les quatre hexagones étant inscrits dans un triangle équilatéral.
Analyse a priori
- Se rendre compte que les trois petits triangles ayant un côté commun avec un côté de l'hexagone sont équilatéraux et égaux (par exemple, observer que chacun d'eux a trois angles égaux : les côtés de l'hexagone régulier sont parallèles aux côtés du grand triangle, et par conséquent les angles d'un petit triangle sont égaux à ceux du grand triangle équilatéral ; on peut aussi les considérer comme supplémentaires aux angles des hexagones réguliers qui valent 120° chacun).
- La longueur des côtés du grand hexagone est donc le tiers de celle des côtés du grand triangle.
- Le grand triangle peut être divisé en 9 triangles équilatéraux égaux (6 formés à partir du centre de l'hexagone et 3 dans la partie restante).
- Connaissant l’aire de l’hexagone, il est donc possible de calculer l’aire d’un de ces triangles : 4158 : 6 = 693 cm2.
- De même, chacun de ces triangles peut être divisé en 9 petits triangles dont 6 inclus dans un petit hexagone : 693 : 9 = 77 cm2.
- L’aire d'un petit hexagone est donc 77 × 6 = 462 cm2. L’aire totale des trois petits hexagones mesure donc : 462 × 3 = 1386 cm2.
Ou bien:
- Observer que chacun des 9 triangles peut être considéré comme composé de 9 petits triangles égaux entre eux. Ainsi, l’hexagone est formé de 54 triangles d’aire 4158 : 54 = 77 cm2. Un petit hexagone a donc une aire de 77 × 6 = 462 cm2. L’aire totale des trois petits hexagones vaut donc 462 × 3 = 1386 cm2.
Ou bien:
- Se rendre compte que l'on peut placer 7 hexagones dans le grand et qu'il reste 12 petits triangles équilatéraux qui forment 2 hexagones de plus. L'aire du grand hexagone est donc égale à celle de 9 petits, ce qui implique qu'un petit hexagone a une aire de 462 cm² (4158/9). Il reste à multiplier ce nombre par 3 pour obtenir la réponse.
Ou bien:
- Considérer que la longueur des côtés des petits hexagones est le tiers de celle des côtés du grand hexagone, l’aire d’un petit hexagone est donc égale à (1/3)2 = 1/9 de l’aire de ce grand hexagone, soit 1/9 de 4158, donc 462 cm2. Les trois petits hexagones auront donc une aire totale mesurant 462 × 3 = 1386 cm2.
Ou bien, Il est possible trouver le résultat exact (1386 cm2) à partir de la formule de l'aire de l'hexagone faisant intervenir des radicaux qui peuvent conduire à des valeurs approchées (par ex. 1385 cm2) s’ils sont remplacés par des approximations décimales.
triangle, hexagone, homothétie, agrandissement, aire
Points attribués, sur 2266 classes de 19 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 7 | 288 (26%) | 127 (12%) | 73 (7%) | 270 (25%) | 343 (31%) | 1101 | 2.23 |
| Cat 8 | 152 (19%) | 87 (11%) | 67 (8%) | 182 (23%) | 305 (38%) | 793 | 2.51 |
| Cat 9 | 33 (17%) | 17 (9%) | 9 (5%) | 34 (17%) | 104 (53%) | 197 | 2.81 |
| Cat 10 | 25 (14%) | 16 (9%) | 15 (9%) | 31 (18%) | 88 (50%) | 175 | 2.81 |
| Total | 498 (22%) | 247 (11%) | 164 (7%) | 517 (23%) | 840 (37%) | 2266 | 2.42 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Selon les critères déterminés lors de l’analyse a priori :
Commentaires
C’est un des rares problèmes de géométrie avec des moyennes supérieures à 2 et avec 60% de réponses correctes.
Les analyses a posteriori seront indispensables si l’on veut connaître la manière dont les groupes ont procédé, ce qui permettra de vérifier les nombreuses hypothèses de l’analyse a priori.
A proposer au Groupe de travail Géométrie plane.
(c) ARMT, 2017-2024