
Banque de problèmes du RMT
gp121-fr
 |
Banque de problèmes du RMTgp121-fr |
|
Reconnaître les triangles formés par les côtés et les diagonales de trapèzes dont les mesures des bases (8 et 12) et de la hauteur (15) sont données, calculer leurs aires et constater qu’elles sont indépendantes de la valeur des angles du trapèze.
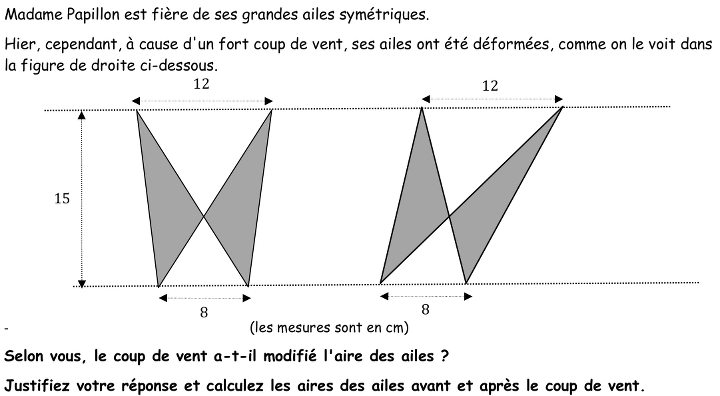
Constater que dans chaque figure on peut distinguer, outre les triangles gris, deux triangles blancs, qui avec les gris constituent un trapèze ; et que les mesures des bases et de la hauteur sont les mêmes pour chacun des trapèzes.
Pour faire la comparaison des aires des deux figures, on peut remarquer que pour chacune des deux figures, les triangles formés par une aile grise et un petit triangle blanc ont une base de 8 cm et la hauteur correspondante de 15 cm, ils ont donc la même aire. En déduire que dans chaque figure, les deux ailes grises ont la même aire. Il reste à les comparer d’une figure à l’autre. On peut aussi travailler avec le grand triangle blanc.
Les procédures et les justifications peuvent être:
1) du genre expérimental avec, par exemple, la reproduction sur une feuille de papier quadrillée les deux figures du papillon et les deux droites parallèles en utilisant les mesures données, 15, 12 et 8, en côtés de carreau. Se rendre compte expérimentalement que pour chaque papillon, les deux ailes se coupent en un point qui est à 6 côtés de carreau du bas et 9 côtés du haut. Vérifier que de telles valeurs sont correctes en calculant l'aire des deux ailes d'un même papillon, on trouve la même valeur (36 carreaux), d’abord en partant de l'aire du triangle formé d'une aile et du petit triangle blanc et en enlevant l'aire de ce dernier, ensuite en partant de l'aire du triangle formé d'une aile et du grand triangle blanc et en enlevant l'aire de ce dernier. En déduire que le coup de vent n'a pas changé les aires des ailes.
2) du genre algébrique, pour le calcul de l’aire d’une aile : Remarquer que les ailes de Madame Papillon sont inscrites dans deux trapèzes de bases 12 cm et 8 cm et de hauteur 15 cm et donc de même aire (A = (12+8)×15/2 = 150 cm2). Quelle que soit la figure considérée, on note a l’aire d’une des deux ailes, h la hauteur du petit triangle blanc, H celle du grand triangle blanc, et A l’aire du trapèze. Pour les deux figures, on a les relations : H + h = 15 ; A = 2a + 4h + 6H et a = 4×15 – 4h. On en déduit l’équation en h : 8×15 – 8h + 4h + 6(15 – h) = 150, d’où h = 6. Pour les deux figures, l’aire d’une aile est donc égale à 4×15 – 4×6 = 36 cm2. Le coup de vent n'a pas changé les aires des ailes.
3) du genre géométrique formel, toujours pour le calcul de l’aire d’une aile par la similitude des triangles, par exemple.
Pour arriver toujours à trouver que les ailes avant ou après le coup de vent ont la même aire qui est, pour chacune, 36 cm2.
géométrie, transformation, aire, Thalès, triangle, trapèze, rapport, constance
Points attribués, sur 1164 classes de 19 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 8 | 509 (64%) | 123 (16%) | 136 (17%) | 15 (2%) | 9 (1%) | 792 | 0.6 |
| Cat 9 | 114 (58%) | 38 (19%) | 32 (16%) | 9 (5%) | 4 (2%) | 197 | 0.74 |
| Cat 10 | 102 (58%) | 32 (18%) | 31 (18%) | 4 (2%) | 6 (3%) | 175 | 0.74 |
| Total | 725 (62%) | 193 (17%) | 199 (17%) | 28 (2%) | 19 (2%) | 1164 | 0.65 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
La réussite très faible, de 0.65, de ce problème, a posé des nombreuses questions au Groupe Géométrie plane, soit sur la gestion de la part des élèves des aspects géométriques du problème, soit sur les critères d'attribution des points qui pourraient avoir poussé beaucoup de correcteurs à ne pas attribuer au moins 1 point là où il y avait un début correct de raisonnement.
La moyenne des points ne rend pas compte de quelques différences significatives d’une section à l’autre.
De l'analyse à posteriori on constate une difficulté, de la part de quelques correcteurs, à interpréter les procédures des élèves, exprimées souvent avec un langage peu formel, lors de la correction des copies de l'épreuve et à attribuer le « 0 », même là où est présent un début de raisonnement correct, comme, par exemple, la recherche et le calcul des aires des trapèzes. Malheureusement cet aspect n'a pas été signalé dans les critères pour le point « 1 » comme il l’est habituellement.
En ce qui concerne le point « 0 », plus que d’une véritable vraie incompréhension, l'analyse à posteriori semble montrer qu'il s’agit « d’erreurs ou d’une gestion insuffisant » du problème.
Les obstacles principaux à la résolution du problème semblent être, pour ceux qui se sont arrêtés à l’aire des trapèzes à ne pas avoir compris la nécessité du passage aux triangles blancs. Ils devaient penser que c’était évident que les triangles aient aussi la même aire.
Et souvent, les élèves n’ont pas compris la nécessité de montrer que les triangles blancs avaient la même hauteur, dont cette justification exigeait le calcul.
En effets, les stratégies indiquées dans l'analyse à priori se sont montrées, pour leur partie formelle, trop ambitieuses. Dans le cas de résolutions correctes, les procédures se sont appuyées, en ce qui concerne la hauteur des triangles, sur le dessin.
L’analyse a posteriori de copies de quelques sections a donné l'impression que les voies de la pratique didactique donnent peu d’espace à des problèmes qui se prêtent aux démarches « inverses », c'est-à-dire aux situations problématique qui ne se résolvent pas par l'application directe de formules, mais qui nécessitent le recours à une réciprocité des raisonnements.
Comme on le sait bien, si dans la pratique de classe on ne va pas plus loin que les notions et des formules qu’on applique d’une manière mécanique, il est difficile de stimuler chez les élèves « la pensée constructive, critique et déductive ».
Des problèmes comme Madame Papillon, utilisés en classe, pourraient mettre les élèves en situation de recherche et la mise en commun pour comparer les solutions de chacun, pourrait ouvrir une route vers des aspects déductifs qui portent à des considérations générales.
On aurait ainsi une activité riche en aspects géométriques avec aussi l’usage d’un langage algébriques, liés entre eux...
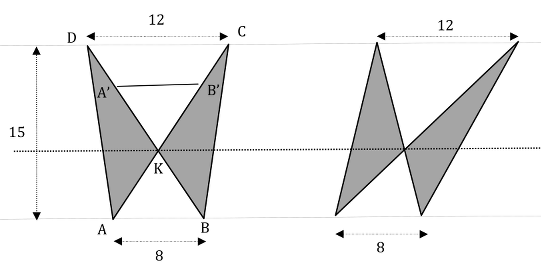
Par exemple, le théorème de Thalès, pourrait trouver une intéressante collocation du type : en posant x = hauteur du petit triangle blanc et 15 – x = hauteur du grand triangle blanc, on obtient l’équation : (15 – x)/x = 12/8 pour trouver x = 6 cm L’aire des triangles blancs est donc, pour le grand : (12 × 9)/2 = 54 cm2, et pour le petit (8 × 6)/2 = 24 cm2. Finalement, calculer l’aire des triangles gris, qui est la même dans la figure symétrique comme dans l’autre, pour chacune des quatre ailes de la figure. Par exemple, partant du triangle formé du petit triangle blanc et d’un triangle gris, on trouve : (8 × 15)/ 2 – 24 = 36 cm2.
Un certain nombre des copies analysées donnent la réponse « non, le coup de vent n'a pas changé l'aire des ailes », d'un point de vue purement intuitif.
(c) ARMT, 2017-2024