Una strana croce

Identificazione

Rally: 25.F.11 ; categorie: 6, 7, 8 ; ambiti: GP, GM
Famiglie:

• IF - Identificare figure
• IF/RC - Riconoscere e costruire figure elementari
• QUA - Lavorare su una quadrettatura
• RD - Ricercare o utilizzare dimensioni

Remarque et suggestion

Sunto

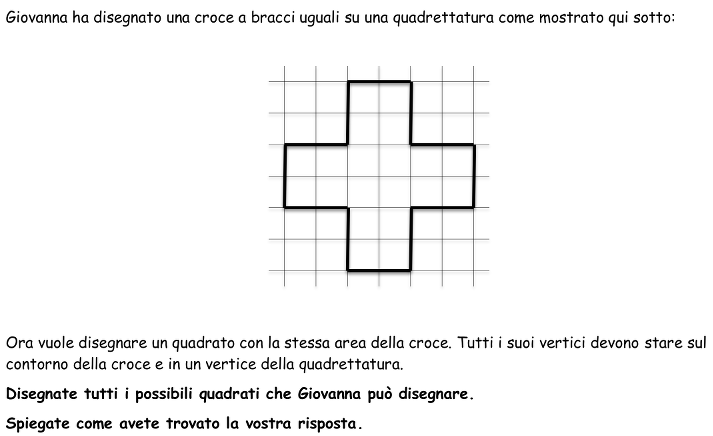
Determinare quali punti del contorno di una croce a bracci uguali disegnata su una quadrettatura possono essere vertici di un quadrato avente la stessa area di quella della croce.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori:

- Capire che si deve costruire un quadrato unendo quattro punti del contorno di una croce su una quadrettatura e che l’area del quadrato deve essere uguale a quella della croce.

- Determinare l’area della croce: scegliere un quadretto della quadrettatura come unità e contare i quadretti contenuti nella croce. L’area è 20 unità.

- Rendersi conto che, poiché 20 non è il quadrato di un numero naturale, i lati del quadrato non potranno seguire la quadrettatura.

- Procedere per tentativi arrivando alle due seguenti configurazioni, che sono due quadrati congruenti:

- Verificare che l’area di un quadrato è esattamente 20 unità confrontando la superficie con quella della croce tramite una compensazione (per esempio un triangolo contenuto nel quadrato è uguale a un triangolo contenuto nella croce, ma non dentro il quadrato), oppure determinando l’area delle figure in esso contenute (per esempio contando i quadretti interi: 12; la superficie restante può essere vista come costituita da 8 triangoli rettangoli metà di un rettangolo 2 × 1 e aventi dunque ciascuno l’area di 1 unità. Si arriva così a 12 + 8 = 20)

Oppure:

Cercare la lunghezza del lato di un quadrato la cui area è 20. A tale scopo cercare un numero il cui quadrato è 20 o il più vicino a 20 (4,5 × 4,5 = 20,25). Costruire un quadrato di lato 4,5 (lati di quadretto), tagliarlo e posizionarlo sulla quadrettatura in modo che i suoi quattro vertici siano sul contorno della croce e dopo aver disegnato il quadrato, verificare che la sua area è precisamente 20 (cfr. la strategia precedente).

Oppure:

Dopo aver disegnato uno dei due quadrati e aver determinato l’area della croce utilizzando il quadretto della griglia come unità di misura, calcolare la misura del lato del quadrato con il teorema di Pitagora: $\sqrt{16+4}$ , e quindi l’area è $\sqrt{20}^2 = 20$.

Risultati

25.F.11

Punteggi attribuiti su 175 classi di 17 sezioni:

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta (disegno dei due quadrati) con giustificazioni chiare e complete (per esempio affermazione che i quadrati sono uguali e determinazione dell’area di uno dei due e confronto con l’area della croce) senza quadrati errati
• 3 punti: Disegno dei due quadrati con giustificazioni incomplete o poco chiare senza quadrati errati
  oppure disegno di uno solo dei due quadrati, con giustificazioni chiare e complete senza quadrati errati
• 2 punti: Disegno dei due quadrati, senza giustificazioni e senza quadrati errati
  oppure disegno dei due quadrati corretti e di un altro errato, ma con giustificazione
• 1 punto: Disegno di un solo quadrato corretto senza giustificazioni
  oppure disegno di due o tre quadrati di cui solo uno corretto con qualche giustificazione
• 0 punto: Incomprensione del problema

(c) ARMT, 2017-2024