Il più bel parallelogramma

Identificazione

Rally: 25.F.19 ; categorie: 9, 10 ; ambito: GP
Famiglia:

• COG - Effettuare una costruzione geometrica

Envoyer une remarque ou une suggestion

Sunto

Costruire un parallelogramma inscritto in un rettangolo, con un vertice equidistante da due lati opposti.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori

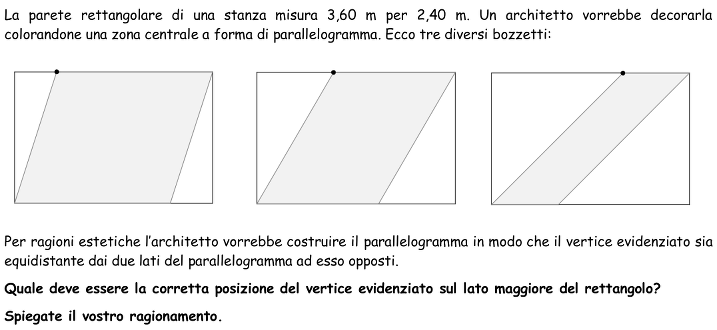
- Comprendere che occorre cercare la posizione di P tale che i segmenti PH e PK abbiano la stessa lunghezza.

- Comprendere che PH = PK implica che PA = PC. A tale conclusione si può arrivare considerando la congruenza dei triangoli APH e CPK (hanno gli angoli congruenti e PH = PK) oppure calcolando l’area del parallelogramma in due modi diversi: PC × PH e PA × PK, da cui segue che PA = PC.

- Procedere per tentativi: dando valori diversi a DP, calcolare AP con il teorema di Pitagora e confrontarlo con PC calcolato per differenza DC−DP. Dopo alcuni tentativi si può trovare che, se DP = 1 m, risulta AP = PC = 2,6 m

Oppure:

- Procedere algebricamente: scegliere un’incognita legata alla posizione di P, ad esempio la misura del segmento DP e cercare di scrivere un’equazione.

Ad esempio, porre DP = x e scrivere l’equazione che traduce la congruenza A P= PC, cioè: $\sqrt{2.4^2 + x^2} = 3.6 -x$ che ha come soluzione x = 1

- Concludere che il parallelogramma cercato ha il vertice P distante 1 m dal vertice D del rettangolo.

Oppure:

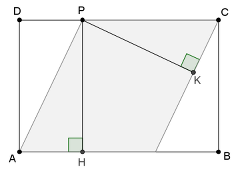
- Procedere geometricamente: comprendere che il parallelogramma, avendo le altezze uguali (o per la congruenza dei triangoli APH e CPK), deve essere un rombo e cercare una possibile costruzione di un rombo di diagonale maggiore AC.

- Trovare il punto medio M di AC e tracciare la retta r per M perpendicolare ad AC. Il punto P è l’intersezione della retta r con il lato CD.

Risultati

14.F.14

Punteggi attribuiti su 40 classi di 6 sezioni:

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta (P dista 1 m da D, o 2,6 m da C, o altra risposta equivalente, oppure costruzione geometrica del punto P) con spiegazioni chiare e complete (tentativi esplicitati oppure procedura algebrica oppure procedura geometrica)
• 3 punti: Risposta corretta con spiegazioni poco chiare o incomplete o con semplice verifica della soluzione
• 2 punti: Risposta corretta senza spiegazione né giustificazione (non costituisce giustificazione la dichiarazione di procedura per tentativi, senza l’esplicitazione dei tentativi stessi né la verifica)
  oppure risposta errata per errore nella risoluzione dell’equazione
• 1 punto: Inizio di ricerca coerente (ad esempio osservata la congruenza dei triangoli)
• 0 punto: Incomprensione del problema