Quadrati su chiodi
Identificazione
Rally:
26.I.05 ; categorie:
3, 4, 5 ; ambito:
GPFamiglie:
Envoyer une remarque ou une suggestion
Sunto
Identificare e contare i quadrati i cui vertici si situano su una parte dei chiodi di un geopiano.
Enunciato
Compito per la risoluzione e saperi mobilizzati
- Capire i vincoli del problema: le figure devono essere dei quadrati i cui vertici coincidono con i chiodi.
La difficoltà, che consiste nel prendere in considerazione dei quadrati in posizione non standard, è in parte superata dall’esempio dato.
- Procedere per costruzioni effettive di quadrati in modo aleatorio. Il rischio è allora di non giungere all’esaustività o di produrre dei doppioni.
Oppure:
- Procedere per costruzioni effettive di quadrati in modo organizzato, per esempio secondo la lunghezza dei lati (quadrato di lato 1, di lato 2, di lato obliquo) o partendo da un punto dato, poi da un altro…
Oppure:
- Conteggio dei quadrati senza costruirli tutti effettivamente, ma descrivendoli in modo chiaro. Questo procedimento può portare a delle dimenticanze.
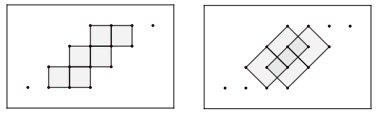
- Una ricerca organizzata porta a trovare:
- 6 quadrati di lato 1 (2 per strisce di punti di larghezza 1)
- 4 quadrati con lati obliqui (diagonali di quadrati)
Risultati
26.I.05
Punteggi attribuiti su 2298 classi di 17 sezioni: :
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|
| Cat 3 | 80 (13%) | 182 (29%) | 52 (8%) | 115 (18%) | 199 (32%) | 628 | 2.27 |
|---|
| Cat 4 | 65 (8%) | 152 (19%) | 65 (8%) | 126 (15%) | 405 (50%) | 813 | 2.8 |
|---|
| Cat 5 | 59 (7%) | 83 (10%) | 45 (5%) | 156 (18%) | 514 (60%) | 857 | 3.15 |
|---|
| Totale | 204 (9%) | 417 (18%) | 162 (7%) | 397 (17%) | 1118 (49%) | 2298 | 2.79 |
|---|
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. |
Secondo i criteri dell’analisi a priori:
- 4 punti: Risposta corretta (10 quadrati) con inventario chiaro: descrizione di tutte le possibilità, disegno di tutti i quadrati o lista esaustiva chiaramente descritta, senza altre figure
- 3 punti: Risposta corretta con inventario poco chiaro: disegno impreciso o lista insufficientemente descritta, senza altre figure
oppure risposta 8 o 9 quadrati (per esempio dimenticanza di due quadrati con lato obliquo) con inventario chiaro, disegno di tutti i quadrati trovati o lista chiaramente descritta, senza altre figure
oppure risposta corretta (10 quadrati) con inventario chiaro di tutte le possibilità, ma con la presenza di una sola figura sbagliata
oppure disegno di tutti i quadrati o lista esaustiva chiaramente spiegata, senza altre figure, ma dimenticata la risposta "10" - 2 punti: 6 o 7 quadrati di cui almeno uno a lato obliquo, senza altre figure
oppure i 10 quadrati e un massimo di due figure errate - 1 punto: 4 o 5 quadrati, senza altre figure
oppure da 6 a 9 quadrati con più di due figure errate - 0 punto: Incomprensione del problema
oppure meno di 4 quadrati con o senza figure errate
