L'Albero di Adele

Identificazione

Rally: 26.II.04 ; categorie: 3, 4, 5 ; ambito: GP
Famiglie:

• AL - Gestire allineamenti di oggetti
• AL/DEN - Enumerare
• RO - Fare pavimentazioni in maniera ottimale
• RO/NU - Fare pavimentazioni con vincoli numerici

Remarque et suggestion

Sunto

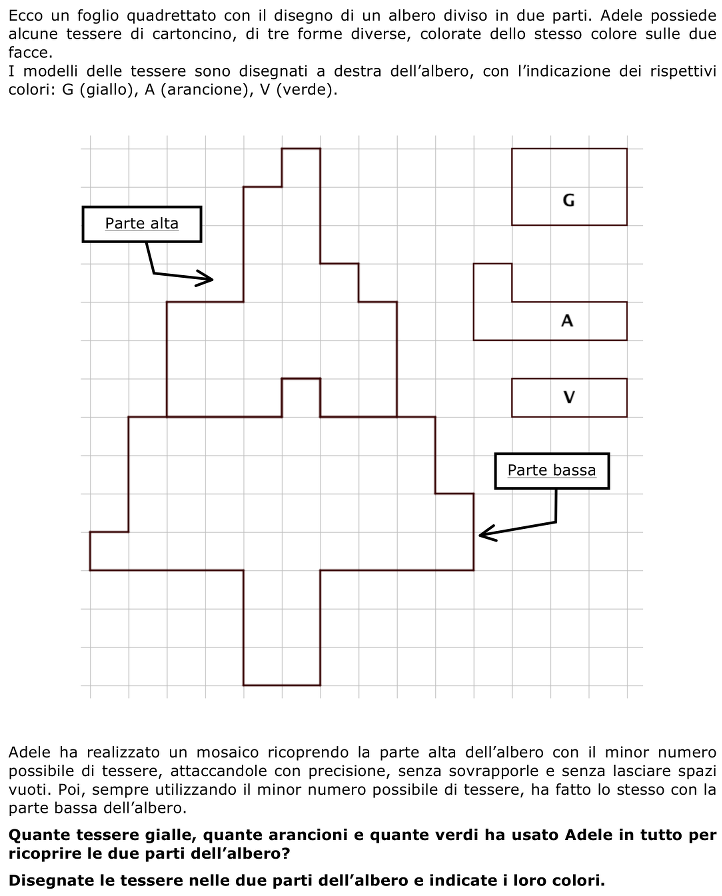
Pavimentare ciascuna delle due regioni in cui è suddivisa una figura disegnata su carta quadrettata con tessere di tre forme date e in modo da minimizzare il numero delle tessere utilizzate in ogni parte.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori

- Comprendere che occorre ricoprire separatamente le due zone dell’albero, utilizzando in ciascuna di esse il minor numero possibile di tessere tra quelle delle tipologie indicate.

- Tenere presente che le tessere non devono uscire dai confini della regione che si vuole ricoprire, che non devono sovrapporsi, né lasciare spazi vuoti.

- Scegliere una regione e provare a ricoprirla, disegnando o posizionando le tessere ritagliate, cercando di usare il minor numero possibile di tessere.

- Procedere per tentativi seguendo l’idea intuitiva (ma da verificare) di sistemare il massimo numero di tessere che occupano più quadretti, cioè le gialle G, che sono rettangoli di 6 quadretti, e poi quelle arancioni A che sono a forma di “L”, (da una parte o dall’altra) ed occupano ciascuna 5 quadretti. Occorrerà verificare ogni volta che lo spazio rimasto, dopo aver sistemato le tessere che occupano più spazio, sia ricopribile con tessere di tipo V (rettangoli di 3 quadretti), altrimenti provare a ridurre il numero di tessere di tipo G o A. Un altro modo di procedere potrebbe essere quello di cercare di posizionare prima tessere arancioni seguendo la linea di confine delle due zone che in alcuni parti "suggerisce" la forma a L di tali tessere.

- Scoprire così che il minimo numero di tessere occorrenti a ricoprire la regione superiore dell’albero è 5: due tessere G, due A e una V (è possibile verificare sperimentalmente che posizionando il numero massimo di tessere G, cioè 3, non si riesce a ricoprire la parte restante con tessere degli altri due tipi).

- Procedere in modo analogo per la regione inferiore dell’albero e trovare che la copertura minimale si ottiene con 4 tessere G, 3 tessere A e una tessera V (è possibile verificare sperimentalmente che posizionando il numero massimo di tessere G, cioè 5, non è possibile completare il ricoprimento utilizzando tessere degli altri due tipi).

- Concludere infine che per il mosaico dell’albero Adele ha usato 6 tessere gialle, 5 tessere arancioni e 2 tessere verdi.

- In figura è mostrato l’albero con le parti alta e bassa pavimentate con una delle possibili disposizioni minimali, rispettivamente, di 5 tessere (2G, 2A, 1V) e di 8 tessere (4G, 3A,1V).

Un errore possibile: considerare la tessera A come una L di 4 quadretti anziché 5 ottenendo quindi un numero di tessere superiore a quello richiesto ed una pavimentazione come quella in figura:

Nozioni matematiche

quadrillage, pavage, figure géométrique, aire, forme, rectangle, polygone, mosaïque

Risultati

26.II.04

Punteggi attribuiti, su 2329 classi di 18 sezioni:

Secondo i criteri determinati durante l’analisi a priori:

• 4 punti: Risposta corretta (6 tessere gialle, 5 tessere arancioni, 2 tessere verdi) con il disegno preciso delle tessere, o un collage, con indicazione del colore delle tessere
• 3 punti: Disegno o collage corretti, ma senza specificare il numero e/o il colore delle tessere
• 2 punti: Risposta non corretta con un disegno o un collage che mostrino il posizionamento corretto e minimale delle tessere su una regione e non minimale sull’altra (con o senza l’indicazione del numero dei pezzi o il loro colore)
• 1 punto: Risposta non corretta dovuta a copertura non minimale di entrambe le regioni
  oppure risposta non corretta dovuta alla presenza di un solo tipo di tessera diverso da quelli dati (per esempio, una “L” di 4 quadrati, anziché di 5)
• 0 punto: Incomprensione del problema (o presenza di più tipi di tessere diverse da quelle date)

(c) ARMT, 2018-2024