
Banque de problèmes du RMT
gp133-fr
 |
Banque de problèmes du RMTgp133-fr |
|
Un triangle est partagé en deux parties de même aire par un segment issu d’un sommet et dont l’autre extrémité se situe sur le côté opposé, dont la longueur est 24 cm. Déterminer la position de cette extrémité sur le côté, sachant encore que la longueur d’un autre côté du triangle est 18 cm.
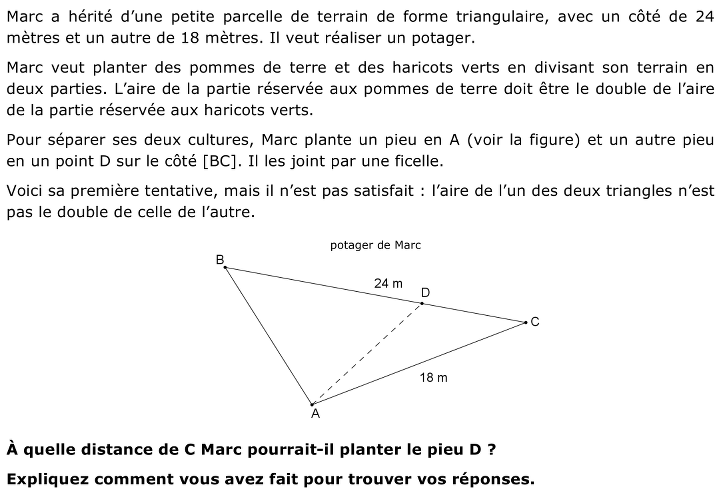
- Se rendre compte que l’énoncé ne fournit que les mesures de deux côtés du triangle ABC et que par conséquent ce triangle n'est pas « déterminé », c'est-à-dire que le triangle dessiné n'est pas le seul à avoir les côtés avec ces mesures.
- Puis réaliser que la surface du potager est indéterminée, tout en notant que les deux triangles ADB et ADC ont une surface indéterminée mais l’une double de l'autre.
- Noter cependant que ces deux triangles ont la même hauteur issue de A. Par conséquent, pour qu'une zone soit le double de l'autre, ils doivent avoir leur base dans le même rapport 2.
- Comprendre que la longueur de la base de 24 m doit donc être divisée en deux parties proportionnelles à 1 et 2. donc BD = 2 DC ou DC = 2 BD.
- En déduire que la borne D doit être plantée à 8 ou 16 mètres de C.
ou : De manière intuitive, vu le manque de données, se contenter de la partition de la base en parties proportionnelles à 1 et 2
triangle, hauteur, aire, proportionnalité, rapport
Points attribués sur 3481 classes de 20 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 6 | 814 (57%) | 207 (14%) | 365 (25%) | 45 (3%) | 6 (0%) | 1437 | 0.76 |
| Cat 7 | 631 (52%) | 199 (16%) | 295 (24%) | 83 (7%) | 9 (1%) | 1217 | 0.88 |
| Cat 8 | 402 (49%) | 147 (18%) | 165 (20%) | 74 (9%) | 39 (5%) | 827 | 1.03 |
| Total | 1847 (53%) | 553 (16%) | 825 (24%) | 202 (6%) | 54 (2%) | 3481 | 0.87 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Comme le montrent déjà les résultats obtenus et rapportés ci-dessus, le problème est très mal réussi e l'analyse a posteriori, tout en nous permettant de comprendre quelles sont les principales raisons des difficultés rencontrées par les élèves, nous oblige, nous, adultes, à réfléchir aux véritables obstacles inhérents au problème.
La difficulté principale de ce problème réside essentiellement dans le manque apparent de données car le triangle n’est pas déterminé (il est général). Il s'agit en fait de la famille des triangles de 24 m de côté et de 18 m de côté, dont la superficie varie de "0" à (24 X 18) : 2. De plus, si le fait central selon lequel la hauteur est la même pour les deux triangles n’est pas saisi, même si elle est indéterminée, dans le cas de la recherche des aires, il est nécessaire de passer par les mesures ou de ne travailler que sur la base.
Le cas des réponses erronées
Dans un certain nombre de copies, en particulier de catégorie 6, où il existe manifestement une incompréhension du problème, les élèves « se sentent obligés » d'utiliser de quelque manière que ce soit les nombres qui apparaissent sur la figure, pour calculer l’aire ou le périmètre du triangle, montrant ainsi également qu'ils ne connaissent pas les propriétés de la figure. De plus, ils ne reconnaissent pas les données qui ne sont pas nécessaires à la résolution du problème, telles que les dimensions du côté AC. Cette mesure est souvent utilisée pour déterminer la longueur inconnue du côté AD, par soustraction ou addition du côté BC.
Dans certains cas, notamment en catégorie 6, il subsiste une confusion entre aire et périmètre. Les élèves travaillent sur le périmètre comme s'il s'agissait de l’aire, dans le sens qu'ils le divisent en deux parties, l'une double de l'autre, pour vérifier ce qui est indiqué dans la déclaration relative aux parcelles destinées respectivement aux pommes de terre ou aux haricots verts. Les unités de mesure de longueur et de surface sont confondues, les mesures sont exprimées indifféremment en centimètres ou en mètres et sont mélangées.
Quand la réponse est correcte
Tant au niveau des catégories 6 que 7, dans la plupart des cas, la réponse correcte, même avec des explications souvent incomplètes, a été donnée en se référant uniquement à la base du triangle.
En effet, si le but principal du problème était de jouer sur la hauteur d'un triangle obtus, externe au triangle lui-même, le fait que la question concerne uniquement la base, a déplacé l'attention des "triangles" sur les "bases".
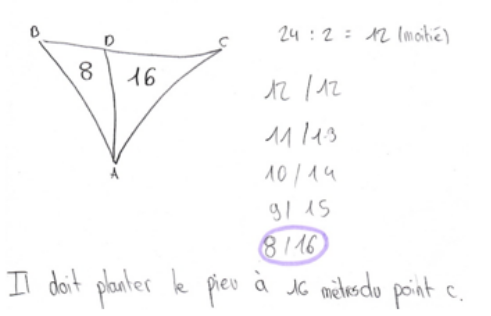
Dans certains cas, il a été suivi d’une procédure partant de la hauteur, suivie de mesures d’échelle et de calculs des zones ou de considérations correctes sur la « relation » entre la base et la surface des deux triangles comme dans l'exemple suivant de catégorie 7.

En partant de la catégorie 7, on trouve des copies ou le théorème de Pythagore a été utilisé pour rechercher la réponse.
Réponses des groupes d'élèves de catégorie 8
Le problème semble devenir vraiment intéressant au niveau de la catégorie 8 où certains groupes d’élèves prennent note de l’aspect « général », comme mentionné ci-dessus, et le résolvent par conséquent avec une procédure générale qui les conduit également à trouver les deux solutions.
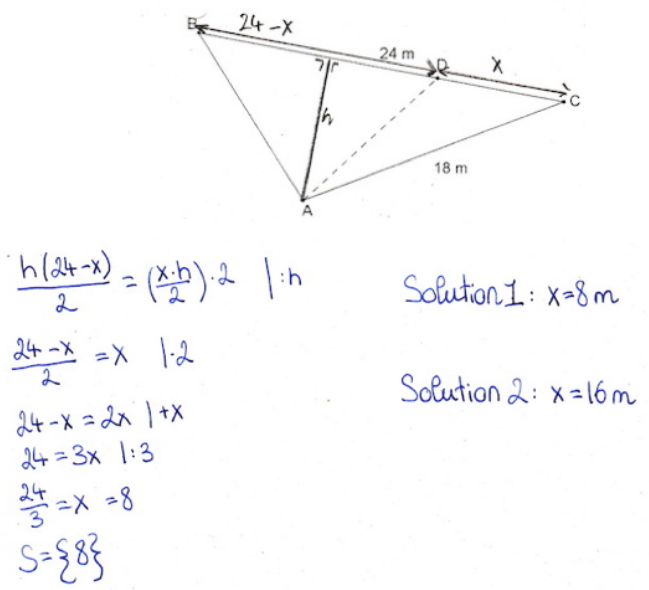
Bien que les cas de réponse avec les deux solutions possibles soient très rares, même dans la catégorie 8, certaines copies, comme celle qui suit, soulignent la compréhension du fait que les triangles en jeu ont la même hauteur.
On peut également noter que le problème n’est pas simple même au niveau de cette catégorie où les résultats sont légèrement meilleurs que ceux des deux catégories précédentes et où la référence à la hauteur pour sa résolution est plus fréquente surtout par rapport à la catégorie 6.
Dans certains cas, les élèves écrivent qu'il est impossible de résoudre le problème car les données sont manquantes. Mais dans un de ces cas (cat. 8), les élèves tentent d'expliquer "l'indétermination"

Le problème du potager, mal réussi dans le contexte de l'épreuve du RMT, revêt un intérêt particulier pour une activité de classe. Son énoncé inclut des aspects de la géométrie qui sont intéressants d'un point de vue pédagogique.
L’énoncé est un concentré d'aspects intéressants sur les propriétés des triangles. Cela peut ouvrir la voie à une discussion constructive sur l’indétermination d’un triangle où les mesures de seulement deux des trois côtés sont connues. Et cette indétermination induit aussi celle de l'aire du triangle. Un autre aspect important est celui lié à la hauteur qui peut être, comme dans ce cas, la même pour les deux triangles qui composent le triangle donné et il n’est pas banal du point de vue didactique, de saisir le rôle de la hauteur d’un triangle obtus.
Il faut revenir à l’analyse de la formule « ab/2 » et aller au-delà de son application algorithmique : « je prends la base et la hauteur qu’on me donne (ou je les mesure) je les multiplie puis je divise par 2 ».
Bien souvent, l’enseignement se limite à faire apprendre cette application mécanique de la formule, sans y consacrer les réflexions nécessaires à sa maîtrise.
Il faut aller rechercher ces lacunes dans le passé des élèves de catégories 6 à 8, dans plusieurs domaines :
- Au moment où a été introduite l’aire du rectangle à partir des longueurs de ses côtés (en nombres entiers) on n’a peut-être pas fait remarquer que la multiplication évoquée n’est pas seulement celle des nombres de carreaux (dans le cas où la base est placée horizontalement sur un quadrillage), mais aussi celle de deux nombres non naturels et, plus encore une opération où deux mesures de longueurs aboutissent à une mesure d’une autre grandeur : l’aire. On a peut-être aussi négligé de faire constater alors que si on double ou triple … la longueur du rectangle, l’aire double ou triple … également ; que c’est la même chose pour la largeur, mais que si on double ou triple ... la longueur et la largeur, l’aire ne double ou ne triple ... pas !
- Au moment d’aborder l’aire du parallélogramme, on n’a peut-être pas fait remarquer que la formule est la même que celle du rectangle.
- Au moment d’aborder l’aire du triangle, on n’a peut-être pas fait remarquer le lien avec la formule de l’aire du parallélogramme ou, tout simplement, que chaque triangle est un demi-parallélogramme et que sa « hauteur » est aussi celle de ce parallélogramme.
- Lors des premières constructions du concept de proportionnalité, on n’a peut-être pas envisagé les cas de « proportionnalité multiples » c’est-à-dire d’une grandeur dépendant de plusieurs autres par une relation multiplicative.
Dans le cas de l’aire du triangle il y a proportionnalité entre les mesures de la base et de l’aire, comme il y a aussi proportionnalité entre les meures de la hauteur et de l’aire. On retrouve le cas du rectangle, mais avec des nombres réels (parce que le modèle des carrée entiers ne fonctionne plus) et avec la division par 2 qui vient se greffer sur le produit, (division loin d’être perçue comme une multiplication par 0,5 ou 1/2 et qui paraît d’une nature différente de la multiplication des deux mesures).
Mais même si toutes ces remarques ont été faites aux moments opportuns, il n’est pas inutile d’y revenir dans une discussion commune sur l’aire du triangle en insistant sur la double proportionnalité - aire et longueur de la base ; aire et mesure de la hauteur-, la nature des grandeurs en jeu et le passage des longueurs aux aires, l’associativité de la multiplication des trois facteurs : les deux mesures et le 1/2, …
En classe, le problème pourrait être complété par une autre question, telle que : Si le plus grand terrain est vendu à 10 000 euros, à combien doit être vendu l’autre, au même prix au mètre carré ? Cette question inciterait les élèves à travailler sur les aires et à ne pas utiliser uniquement le rapport au sein de la base.
Études / Approfondimenti. L’orto I – Le potager I, I membri del sottogruppo “per i grandi” del Gruppo geometria. IN La Gazzetta di Trasalpino n.9, 2019 pp 141-160.
(c) ARMT, 2018-2024