
Banque de problèmes du RMT
gp145-fr
 |
Banque de problèmes du RMTgp145-fr |
|
Calculer le rapport des aires de deux types de figures d’une mosaïque, par décompositions en demi-carrés triangulaires et rectangles dont un côté est celui d’un carré et l’autre celui de sa diagonale.

- Imaginer la paroi à partir de la figure donnée et comprendre, vu la disposition des carreaux, que le nombre des gris et des blancs est approximativement le même sur une paroi constituée de milliers de carreaux et qu’il suffit donc de calculer l’aire d’un seul carreau gris et d’un seul carreau blanc pour déterminer le rapport entre les parties en blanc et en gris de la paroi.
- Observer attentivement les deux polygones, vérifier qu’ils ont chacun 16 côtés, disposés sur une trame carrée. Les carreaux gris occupent un carré de la trame et quatre petits triangles, empruntés aux carreaux blancs. (voir figure 1). Observer encore que les carreaux gris peuvent être considérés comme la superposition de deux carrés dont les côtés respectifs forment des angles de 45 degrés (ou qu’on peut passer de l’un à l’autre par une rotation de 45 degrés). Par conséquent on peut être certains que tous les angles aigus du polygone gris sont droits.
- Passer à l’analyse du pourtour des carreaux et noter que chaque côté d’un carré de la trame est composé de deux des 16 côtés du polygone, de 5 cm de longueur et d’une diagonale d’un triangle isocèle rectangle dont deux côtés mesurent aussi 5 cm.
- A la suite de ces observations, on peut envisager les aires des carreaux comme celles de l’aire du carré de la trame en y ajoutant ou y retranchant respectivement pour le carreau gris et pour le carreau blanc, celles des quatre triangles.
- Passer au calculs des aires des deux carreaux :
en cm : diagonale d’un triangle, 5√2 o √50 ≅ 7,07; côté d’un carré de la trame : 10 + 5√2 ≅ 17,07
en cm2: aire de quatre triangles 4(25/2) = 50; aire d’un carré de la trame (10 + 5√2)2 = 291,42… ≅ 290
aire d’un carreau gris ou blanc (10 + 5√2)2 + 50 ≅ 340 ou (10 + 5√2)2 - 50 ≅ 240
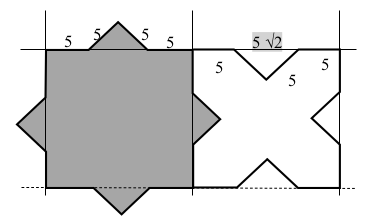
- Calculer finalement le rapport des aires en blanc et en gris ; c’est-à-dire « aire d’un carreau blanc »/« aire d’un carreau gris »: [(10 + 5√2)2 – 50 ]/ [(10 + 5√2)2 + 50] ≅ 240/340 ≅ 0,7 (La réponse exacte serait √2/2 pour ceux qui sont capables d’effectuer les simplifications nécessaires) .
Ou, chercher à décomposer chacun des carreaux par des carrés, rectangles et petits triangles, et effectuer les calculs des aires correspondantes
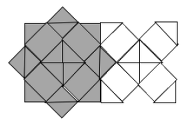
Voici quelques exemples de ces pavages où il s’agit de reconnaître les côtés de longueur 5 et ceux de longueur 5√2 ou √50. :
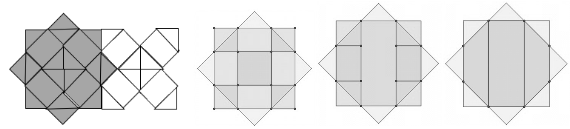
Dans le premier exemple (figure 2) le carreau gris se décompose en 16 triangles (isocèles rectangles) et 4 rectangles, le carreau blanc en 8 triangles et 4 rectangles. Les aires des triangles sont égales à 12,5 = 25/2 cm2. Les rectangles ont 5 cm de largeur, leur longueur est celle de l’hypoténuse d’un triangle qui peut se calculer par Pythagore ou comme le côté du carré central : √50 cm qu’on peut arrondir à 7,0 ou 7,1. L’aire d’un rectangle est donc 5 x √50 ≅ 35 ≅ 35,5.
aire, polygone, mesure, longueur, Pythagore, rapport, pavage, carré, triangle, rectangle, diagonale
Points attribués sur 1209 classes de 18 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 8 | 436 (54%) | 201 (25%) | 79 (10%) | 44 (5%) | 49 (6%) | 809 | 0.85 |
| Cat 9 | 93 (45%) | 50 (24%) | 18 (9%) | 19 (9%) | 27 (13%) | 207 | 1.21 |
| Cat 10 | 63 (33%) | 41 (21%) | 28 (15%) | 24 (12%) | 37 (19%) | 193 | 1.64 |
| Total | 592 (49%) | 292 (24%) | 125 (10%) | 87 (7%) | 113 (9%) | 1209 | 1.04 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
1.1 Perception de la trame des carreaux
Dans la majorité des cas la mosaïque est perçue sur une trame carrée. Les carreaux gris occupent un carré de la trame et quatre petits triangles, empruntés aux carreaux blancs. (voir figure 3). Chaque côté de ce carré est composé de deux des 16 côtés du polygone, dont la longueur mesure 5 cm et de l’hypoténuse d’un triangle.
Il suffit alors de déterminer la longueur de l’hypoténuse d’un petit triangle (√50 ≅ 7,07) puis le côté d’un carré de la grille (10 + √50) ≅ 17,07 (en cm) pour calculer l’aire de ce carré (10 + √50)2 ≅ 291,42 (en cm2).
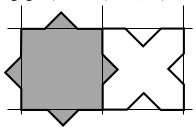
1.2. Les erreurs de perception des « carrés de la grille » ou des décompositions
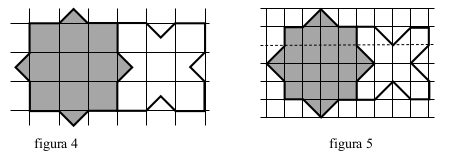
De nombreux groupes font confiance à leur perception visuelle des pourtours des carreaux ou des côtés des « carrés de la grille » sans analyse « métrique » des segments qui les composent. La majorité perçoivent un partage en 9 parties isométriques (3 x 3), (figure 4) d’autres en 16 parties (4 x 4) (figure 5). Dans le cas de la figure 4, le carré de la grille a 15 cm de côté et son aire est de 225 (en cm2).
Une copie a choisi 6 cm comme partie centrale du côté du carré de la grille, faisant apparaître des triangles isocèles considérés comme des demi-carrés de côtés 5 et 5 et 6 cm, d’aire 9 cm2.
1.3. Décomposition en triangles et rectangles
Dans les rares cas de décomposition en 8 triangles et 4 rectangles pour le carreau blanc, 16 triangles et 4 rectangles pour le carreau gris, on trouve le rapport visuel erroné « un rectangle vaut deux triangles » pour aboutir, après substitution à 16 triangles blancs et 24 triangles gris et à un rapport des aires 16/24 = 2/3. Ou on arrive à conter 22 triangles pour le carreau gris et 14 pour le carreau blanc. On arrive ensuite au rapport 7/11.
2. Difficultés dans les calculs des longueur et aires
Dans quelques copies de la catégorie 1.1 ci-dessus, les élèves aboutissent à des aires respectives de ≅ 241 et ≅ 341 cm2 pour les carreaux blancs et gris. D’autres présentent des confusions des oublis ou des erreurs dans le calcul de la diagonale ou de l’aire des petits triangles.
Par exemple : aire du carreau blanc 241,42 aire du gris 291,42 (l’aire des 4 triangles n’a pas été ajoutée pour le carreau gris).
En ce qui concerne les copies de la catégorie 1.2 ci-dessus, une partie des élèves aboutissent à des aires respectives de 175 et 275 cm2 pour les carreaux blancs et gris, calculées à partir de celle du carré de la grille 152 = 225. Les autres présentent des incohérences ; on y trouve bien les 225 cm2 du carré de la grille mais les aires des quatre triangles à ajouter ou retrancher n’apparaissent pas. Il y a en effet une difficulté supplémentaire due à la perception erronée de la grille (3 x 3) : les hypoténuses de 5 cm ne s’accordent pas avec les côtés de 5 cm des autres côtés. Dans un cas, ces triangles sont considérés comme équilatéraux.
3. Difficultés dans le calcul du rapport
Les deux aires des carreaux ont été trouvées par une partie des groupes, correctement (1.1) ou avec l’erreur de perception visuelle (1.2) ; mais la réponse à la question « Calculez le rapport entre les aires en blanc et en gris de la paroi. » n’est pas toujours correcte.
Dans certains cas, le calcul des aires est étendu à celles de la vingtaine de carreaux, complets ou incomplets, de la figure de l’énoncé, sans prêter attention à la « paroi entière » ni avoir compris qu’il suffit de comparer les aires d’un seul carreau gris et d’un seul carreau blanc.
On trouve aussi plusieurs rapports inverses ou non justifiés.
Réponses très partielles
Dans ces copies, il y a des tentatives de décomposition des carreaux toutes différentes et incomplètes, difficiles à relier aux autres catégories.
Observations
La moyenne de « 0,8 » points attribués peut sembler faible, mais il faut rappeler ici que la réponse du problème est la synthèse de toutes les tâches de résolution et il faut donc s’intéresser à chacune d’entre elles plutôt qu’à une tâche « globale ».
La première tâche mentionnée dans la rubrique « Tâche de résolution et savoirs mobilisés » consistant à se limiter à la comparaison des aires d’un seul carreau gris et d’un seul carreau blanc, présente une difficulté pour un tiers des élèves environ. On la considère comme « allant de soi » pour un adulte mais il ne faut pas oublier que ce rapport n’est qu’une approximation dépendant du nombre de carreaux de la paroi entière estimé, dans l’énoncé du problème, par « des milliers de carreaux gris et de carreaux blancs ».
La deuxième tâche est d’analyser et décomposer les deux carreaux, en comparant les longueurs des segments du partage (côtés du polygone de 5 cm et autres côtés des triangles, carrés et rectangles) indépendamment des perceptions visuelles. C’est là qu’apparaît un obstacle que nous devrons chercher à mieux définir.
La troisième tâche est celle des calculs d’aire, avec, en préambule la détermination de la longueur de l’hypoténuse du triangle isocèle rectangle 5, ?, 5. La grande majorité des groupes qui l’ont calculée sont arrivés à « 7,07 » par le théorème de Pythagore mais on peut se poser des questions sur la nature de cette écriture « 7,07 ». Dans certains cas, elle est précédée de √50, d’autres fois de √(25 + 25) ou encore de √(52 + 52 ) mais très rarement suivie d’un signe d’approximation « ≅ ». Dans deux cas où cette diagonale a permis de déterminer l’aire d’un carré central de la décomposition (figure 6), le résultat est 7,072 = 49,98 au lieu de 50.
L’application du théorème de Pythagore semble encore algorithmique et se déroule dans le temps : 52 suivie de + 52 et de 52 + 52 avant de passer à la mention de la √ . On ne relève jamais l’écriture 2 x 52 qui pourrait exprimer que l’aire du carré construit sur l’hypoténuse est le double de l’aire des carrés construits sur les côtés de l’angle droit ; comme on ne relève jamais l’écriture 5√2.
C’est au niveau de la catégorie 10 qu’on trouve quelques cas de calculs avec partout √2, aussi pour le rapport.
La quatrième tâche, du calcul du rapport, dépend évidemment de la réussite des précédentes. Les réponses différentes de celles que l’adulte attend sont vraisemblablement dues à l’interprétation du mot « rapport » et de l’ordre des deux grandeurs qui le déterminent.
Ce problème plutôt « riche » se prête à développer en classe des sujets allant de l'analyse approfondie du triangle rectangle isocèle qui entraine Pythagore, aux nombres irrationnels, à l'approximation, à l’approximation, mais aussi à la comparaison des aires.
En ce qui concerne le triangle rectangle isocèle, la configuration "particulière" de la mosaïque en question a conduit un certain nombre de groupes d'élèves à "faire confiance" au premier regard et par conséquent à ne pas relier ce qu'ils ont vu sur la figure aux propriétés du triangle rectangle isocèle, en considérant que les trois côtés mesuraient 5 cm.
En classe, il pourrait être intéressant d'aborder le problème, par exemple avec un agrandissement de la figure, et d'engager un débat sur le triangle, en référence au point 1.2., décrit ci-dessus.
(c) ARMT, 2019-2024