Il tavolino del nonno

Identificazione

Rally: 27.F.19 ; categorie: 9, 10 ; ambiti: GP, GM
Famiglie:

• CA - Confrontare aree
• CA/P - Confrontare aree su una quadrettatura

Envoyer une remarque ou une suggestion

Sunto

Data una griglia di 23 × 23 quadrati unità, con un inizio di pavimentazione con poligoni chiari e scuri (rettangoli scuri di area 4 quadrati unità, singoli quadrati unità scuri e trapezi chiari di area 2 e 1,5 quadrati unità), confrontare le aree delle parti chiare e scure immaginando di completare la pavimentazione.

Enunciato

Compito per la risoluzione e saperi mobilizzati

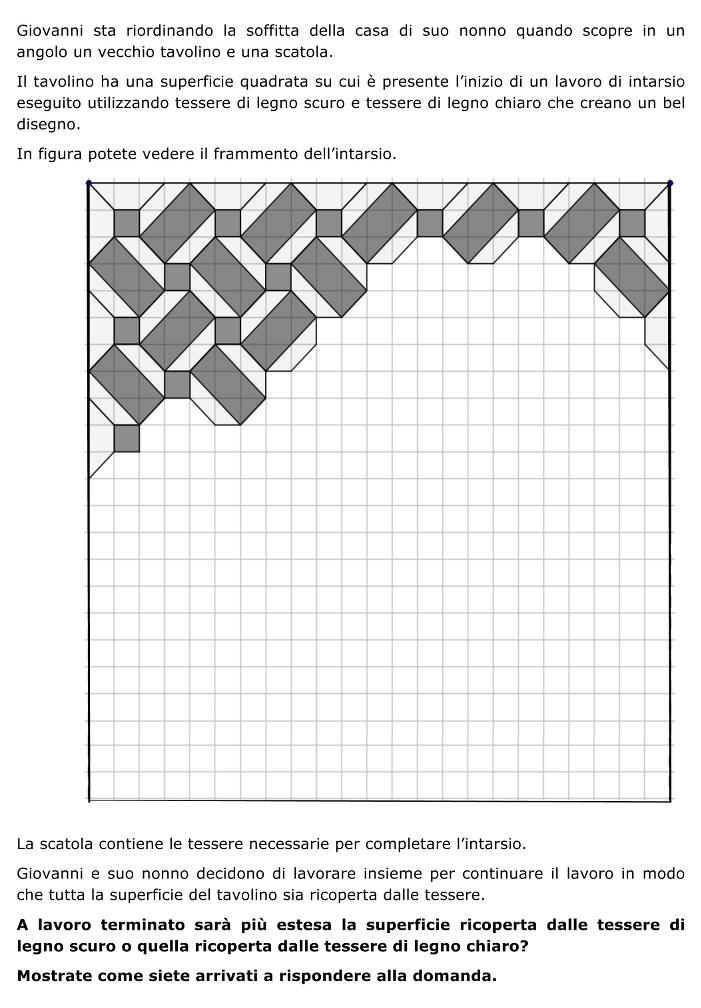
Analisi a priori:

- Osservare la figura, riconoscere che si tratta di un motivo regolare che si ripete su una quadrettatura di 23×23, il cui bordo ha un motivo differente.

- Completare la figura, poi contare 36 e 25 quadratini (quadrati unità) e 60 poligoni (ottagoni) per sistemare i 60 rettangoli, ciascuno di area 4 quadrati unità. Trovare che l’area scura è di 301 quadrati unità, quindi superiore all’area bianca che è di 23 × 23 – 301 = 228 quadrati unità

Oppure

- Osservare che la decorazione è composta da poligoni chiari e scuri, valutare la loro area utilizzando come unità il quadretto della griglia e contarli in modo da calcolare l’area totale delle superfici chiara e scura. Un’osservazione precisa permette di identificare rettangoli R (area 4) e quadrati Q (area 1) scuri; trapezi T1 (area 1,5) e trapezi T2 (area 2) chiari, questi ultimi presenti solo sul bordo.

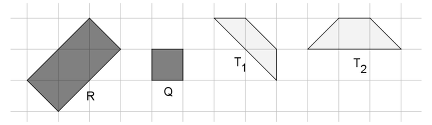
- Ci sono diversi modi di determinare l’area scura e l’area chiara raggruppando per motivi (ottagoni, triangoli, quadrati, trapezi). Ecco due esempi: Contare il numero di ottagoni che contengono il rettangolo nero, il numero di quadretti neri, il numero di trapezi T2: ce ne sono 6 per ogni lato del tavolino, cioè 24 in totale che rappresentano 48 quadrati-unità.

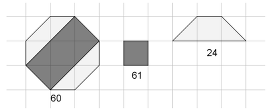
- Per contare gli ottagoni, si può osservare che la prima fila ne contiene 5 e che la seconda, una volta completata, ne avrà 6. Ci sono quindi 11 ottagoni per questo motivo che si ripete 5 volte su 21 quadretti in altezza, e resta una fila di 5 ottagoni sugli ultimi tre quadretti, che porta il loro numero a 60 ottagoni. In modo analogo si contano i quadrati Q: 11 × 5 + 6 = 61.

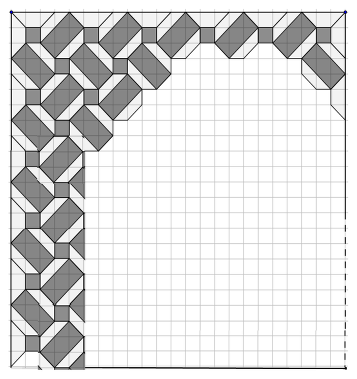
- Concludere che la parte scura ha area 301 (4 × 60 + 61) e quella chiara ha area 228 (2 × 1,5 × 60 + 2 × 24).

Oppure

- Osservare che in ogni ottagono il numero dei quadretti neri (4) è maggiore di quelli chiari (3) di una unità e quindi in tutto la parte scura degli ottagoni supera di 60 unità quella chiara, mentre l’area chiara dei trapezi T2 è soltanto di 48 quadrati unitari. Concludere che la parte scura ha un’area superiore a quella della parte chiara.

Nozioni matematiche

pavimentazione, area, poligono, unità

Risultati

27.F.19

Punti attribuiti su 53 classi di 9 sezioni:

Secondo i criteri determinati nell’analisi a priori:

• 4 punti: Risposta corretta (è più estesa la superficie ricoperta da legno scuro) con un disegno completo e determinazione dell’area per conteggio delle 301 unità, o con la descrizione chiara e dettagliata del procedimento seguito e dei calcoli fatti
• 3 punti: Risposta corretta con un disegno completo senza il conteggio delle 301 unità, o con spiegazioni incomplete o poco chiare (ad esempio sono presenti i calcoli ma non è descritto chiaramente come si è effettuato il conteggio)
• 2 punti: Disegno incompleto, ma che mostra una procedura corretta
  oppure ragionamento corretto ma procedura contenente un errore di calcolo, con una risposta corretta o errata
• 1 punto: Inizio di ragionamento e di conteggio corretti, oppure risposta senza spiegazione
• 0 punto: Incomprensione del problema