I due quadrati

Identificazione

Rally: 29.I.18 ; categorie: 8, 9, 10 ; ambiti: GP,
Famiglie:

• CA - Confrontare aree
• DEM - Fare una dimostrazione
• GDE - Organizzare una successione di relazioni in geometria deduttiva
• TR - Costruire, utilizzare e/o effettuare una trasformazione geometrica

Envoyer une remarque ou une suggestion

Sunto

Giustificare che, facendo ruotare un quadrato intorno ad uno dei suoi vertici, situato al centro di un altro quadrato uguale, l’area dell’intersezione dei due quadrati è costante.

Enunciato

Compito per la risoluzione e saperi mobilizzati

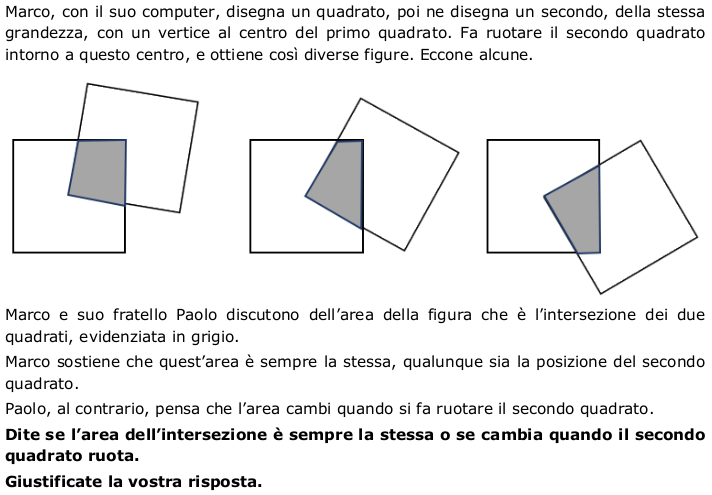
Analisi a priori:

- Immaginare la rotazione del secondo quadrato (o realizzarla con l’aiuto di uno dei quadrati ritagliati) e constatare che l’intersezione cambia forma, poi trovare che questa intersezione è un quadrilatero ma che può anche essere essa stessa un quadrato o ancora un triangolo.

- Confrontare le aree dei due casi particolari in cui l’intersezione è un quadrato e quella in cui l’intersezione è un triangolo e constatare che, in ciascuno dei due casi, l’area è un quarto del quadrato intero.

- Nel caso generale, (in cui si sia fatto ruotare il quadrato di un angolo qualunque, osservare l’intersezione e constatare che l’intersezione è sempre un quadrilatero in cui due angoli sono retti e due lati sono uguali (ottenuti con una rotazione di $90$ gradi intorno al centro di rotazione, AB e AC sulla figura qui a lato). Dedurne che i due triangoli rettangoli (AKB e AHC sulla figura) sono uguali, e anche le loro aree, e che il triangolo «ritagliato» su un lato dell’intersezione è compensato dal triangolo «aggiunto» dall’altra parte.

Oppure

- Misurare le dimensioni delle tre intersezioni (o scegliere misure ipotetiche) e calcolare le loro aree (per esempio come somma dell’area dei due triangoli AQC e AQB della figura a lato). Confrontare queste tre aree e trovare che esse sono uguali, (rendendosi conto che si tratta di approssimazioni).

Ci sono ancora altre partizioni del quadrilatero e ci sono altre partizioni dei quadrilateri intersezione o altri modi di convincersi che l’area dell’intersezione resta costante.

L’approccio della «dimostrazione» geometrica potrà essere oggetto delle indicazioni didattiche di questo problema in cui l’area dell’intersezione è costante qualunque sia il valore dell’angolo di rotazione.

Nozioni matematiche

quadrato, area, rotazione, deduzione, intersezione, quadrilatero, triangolo, angolo, dimostrazione

Risultati

29.I.18

Punti attribuiti su 752 classi di 21 sezioni:

Secondo i criteri determinati nell’analisi a priori:

• 4 punti: Risposta corretta (l’area dell’intersezione è sempre la stessa) dichiarando che l’area è quella di un quarto del quadrato (uno dei casi particolari, oppure di un triangolo equivalente per l’altro caso particolare), e una giustificazione che parli della compensazione dei triangoli per il caso generale.
• 3 punti: Risposta corretta con spiegazione che l’area è sempre la stessa, ma giustificazione limitata ai tre esempi e non al caso generale, o aggiungendo “a partire dalle misure prese sulle figure”, e esplicitando che si tratta di approssimazioni “che si devono considerare come uguali”.
• 2 punti: Risposta sì, con spiegazione per uno soltanto dei casi particolari (e il caso generale non citato oppure considerato come evidente)
  oppure a partire dalle misure prese sulle figure senza citare le approssimazioni che si devono considerare come uguali.
• 1 punto: Risposta corretta senza spiegazioni
  oppure solo la constatazione dell’esistenza del caso particolare “quadrato” e/o “triangolo
  oppure risposta sbagliata (l’area cambia) a causa di misure sbagliate prese dalle figure
  oppure risposta sbagliata (l’area cambia) con una traccia di spiegazione che mostri l’inizio di una ricerca coerente ma con errori.
• 0 punto: Incomprensione del problema.