Il gatto sul tetto

Identificazione

Rally: 30.I.19 ; categorie: 8, 9, 10 ; ambiti: GP, GM, 3D
Famiglie:

• LA - Utilizzare misure di lunghezze e aree
• LAV - Gestire lunghezze, superfici, volumi
• LAV/LA - Misurare o calcolare lunghezze e/o aree
• RD - Ricercare o utilizzare dimensioni
• RD/AP - Determinare aree e/o perimetri

Remarque et suggestion

Sunto

Determinare la misura dell’ipotenusa di un triangolo rettangolo, noti un cateto e i lati di un rettangolo con i vertici uno sull’ipotenusa e due su uno dei cateti. Sfruttare la similitudine di due triangoli.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori

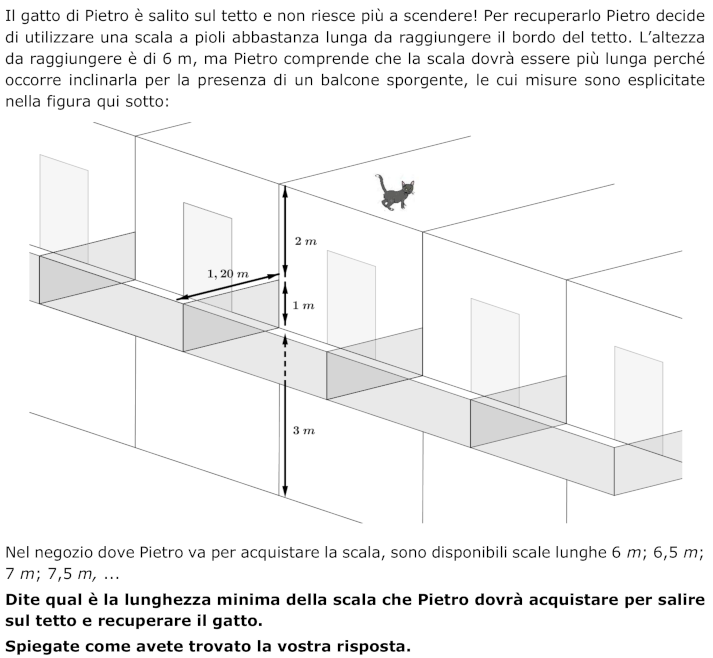
- Appropriarsi della situazione pensando al posizionamento della scala con la base sul terreno antistante la parete e l’estremità sul bordo del tetto.

- Comprendere che ci sono varie posizioni per la scala e che quella più vantaggiosa (di lunghezza minima) è quella che, pur evitando il balcone, vi si avvicina il più possibile, fino a toccarlo sul bordo superiore.

- Modellizzare la situazione da un punto di vista matematico (vedi figura): si tratta di determinare l’ipotenusa AE di un triangolo rettangolo, noti un cateto AB e le misure dei lati di un rettangolo con i vertici uno sull’ipotenusa e due su uno dei cateti: 1,20 m e 1 m, in grigio nella figura.

- Capire che alcuni dati sono superflui e che per determinare la misura di AE occorre riconoscere la similitudine dei triangoli ADC e AEB.

- Osservare che il rapporto di similitudine è 3 (i lati del triangolo AEB sono il triplo di quelli del triangolo ADC).

- Determinare la misura di AE utilizzando la similitudine (rapporti o proporzioni) e il teorema di Pitagora, ottenendo il valore AE≈6,997 m.

Oppure

- Fare un disegno in scala del triangolo e del rettangolo inscritto (per esempio AB = 6 cm, CD = 1,20 cm) e misurare la lunghezza dell’ipotenusa AE. Rapportare il valore ottenuto alle dimensioni originali ottenendo un valore di poco inferiore a 7 m

- Concludere che la scala deve avere una lunghezza di almeno 7 metri.

Nozioni matematiche

rettangolo, triangolo, similitudine, lunghezza, proporzionalità, Pitagora

Risultati

30.I.19

Punteggi attribuiti su 1098 classi de 20 sezioni:

Secondo i criteri dell'analisi a priori :

• 4 punti: Risposta corretta (la lunghezza minima della scala è 7 m) con spiegazione chiara e completa che metta in evidenza la similitudine e la proporzionalità tra le varie misure oppure con un disegno in scala e misure accuratamente prese su di esso
• 3 punti: Risposta corretta con spiegazione incompleta o poco chiara
  oppure procedimento corretto e ben descritto fino alla determinazione della misura di AE, ma risposta mancante
• 2 punti: Risposta errata (6,5 m o 7,5 m) per un errore di calcolo, ma procedimento corretto
• 1 punto: Risposta errata (7,5 m) per un errore di misura
  oppure inizio di ricerca coerente (ad esempio: applicazione del teorema di Pitagora nel triangolo ADC)
  oppure risposta corretta senza alcuna spiegazione
• 0 punto: Incomprensione del problema

(c) ARMT, 2022-2024