Girandola di triangoli

Identificazione

Rally: 31.I.16 ; categorie: 7, 8, 9, 10 ; ambito: GP
Famiglie:

• CA - Confrontare aree
• DEC - Ritagliare e/o assemblare figure

Envoyer une remarque ou une suggestion

Sunto

A partire dall’immagine di quattro triangoli rettangoli identici, attraverso un giudizioso riposizionamento delle parti, trovare l’area esatta di un triangolo di cui sono noti la misura dell’ipotenusa (7 cm) e la differenza tra i cateti (1 cm).

Enunciato

Compito per la risoluzione e saperi mobilizzati

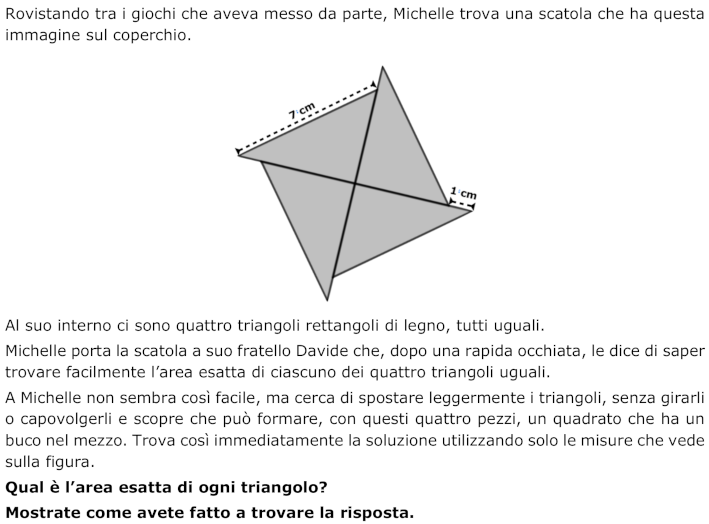
- Comprendere la situazione: i quattro triangoli sono rettangoli e tutti uguali, hanno l’ipotenusa lunga 7 cm e un cateto che è lungo 1 cm più dell’altro; costruendo un quadrato di lato 7 cm con tutti i triangoli si deve trovare l’area di un triangolo.

- Capire che per poter costruire un quadrato di lato 7 cm è necessario che i suoi lati siano le ipotenuse dei quattro triangoli.

- Mediante il ritaglio e la composizione dei triangoli oppure disegnando, cercare di costruire il quadrato e accorgersi che l’unico modo per riuscirci è quello di lasciare, al centro, un quadrato vuoto di lato 1 cm

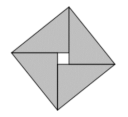
Trovare l’area del quadrato costruito (7 × 7 = 49 in cm$^2$) e togliere l’area del quadrato vuoto (1 × 1 = 1 in cm$^2$) per trovare l’area dei quattro triangoli (49 – 1 = 48 in cm$^2$). Essendo i triangoli tutti congruenti, basta dividere l’area totale per 4, per trovare l’area di un triangolo (48 ÷ 4 = 12 in cm$^2$)

Oppure, per via algebrica, indicare con x e x + 1 le misure dei cateti, risolvere l’equazione x2 + (x + 1)2 = 49 e calcolare l’area del triangolo sostituendo i valori trovati nella formula x (x + 1) ÷ 2.

Nozioni matematiche

quadrato, triangolo, triangolo rettangolo, area, lunghezza, misure di lunghezza, deduzione, equivalenza, decomposizione, similitudine, rapporto, isometria, traslazione, rotazione

Risultati

31.I.16

su 2461 classi di 20 sezioni

Secondo i criteri dell’analisi a priori :

• 4 punti: Risposta corretta “area del triangolo = 12 cm$^2$”, senza alcuna approssimazione con descrizione chiare e completa (ricostruzione precisa del quadrato, dettagli e giustificazione dei calcoli)
• 3 punti: Risposta corretta, senza alcuna approssimazione con descrizione poco chiara o incompleta
  oppure risposta compresa tra 11,88 e 12,38 o 12,375 (in cm$^2$) dovuta ad un’approssimazione, con descrizione chiara e completa (dettagli e giustificazione dei calcoli) OPURE risposta “48” (dimenticanza della divisione per 4) con descrizione chiara e completa
• 2 punti: Risposta corretta senza spiegazioni
  oppure risposta compresa tra 11,88 e 12,38 o 12,375 (in cm$^2$) dovuta ad un’approssimazione, con descrizione poco chiara o incompleta (calcoli incompleti o non giustificati)
• 1 punto: Inizio di ragionamento corretto, per esempio trovata l’area del quadrato di lato 7 cm
  oppure risposta errata: trovata l’area di un triangolo 12,25 cm$^2$ (49 ÷ 4) e dimenticando di togliere il centimetro quadrato centrale
• 0 punto: Incomprensione del problema