
Banque de problèmes du RMT
gp24-fr
 |
Banque de problèmes du RMTgp24-fr |
|
Analyser une suite de demi-cercles alignés en alternance dont les diamètres successifs (256, 192, 144, …) sont en progression géométrique. Trouver la somme de ces termes et la longueur du chemin déterminé par les arcs de cercles.

La tâche de résolution nécessite la maîtrise de connaissances de différents domaines conceptuels, allant de l'arithmétique (suites et calcul de la somme de termes d'une progression géométrique) à la géométrie (longueur du cercle, théorème de Thales, similitude) et à une approche de l’analyse.
Il y a plusieurs moyens de trouver la distance demandée (en ligne droite) :
1) On peut penser à calculer le rapport - dont on parle dans l’énoncé d’un diamètre au suivant et observer qu’il est constant : 256/192 = 192/144 = 144/108 = … = 4/3 et, à partir de cette constatatione trouver les termes suivants de la suite et calculer une approximation de la somme des termes de la suite : 256 + 192 + 144 + 108 + 81 + 60,75 + 45,5625 + à la calculatrice. (On arrive à 966 après 10 termes, 1010 après 15 termes, 1020 après 20 termes, 1023 après 25 termes, …). Et ceci permet d’observer que : à mesure que le nombre de termes augmente, la somme augmente très peu et ne différera donc pas beaucoup de 1023.
L’écriture formelle des deux sommes
S = 256 + 256 (3/4) + 256 (3/4)2 + … et (3/4) S = 256 (3/4) + 256 (3/4)2 + … et de leurs différence
S - (3/4) S = 256, permet de passer à l’équation (dont l’inconnue est S) S/4 = 256 et de conclure S = 1024.
2) On peut recourir aux connaissances de la similitude et des homothétiesen constatant que, de part et d'autre de l'axe, les demi-cercles sont homothétiques et que le centre d’homothétie est l’extrémité de la queue.
2.1) Par un dessin géométrique précis, on peut obtenir la mesure, avec une bonne approximation, du segment ayant comme extrémités A et P (point d’intersection entre l’axe qui part de A et la tangente aux demi-cercles.
2.2) Ou, par le recours au théorème de Thales (voir la figure ci-dessous), prendre en considération le rapport d/128 = (d - 224)/96, d’où d = 996 et la mesure de la distance demandée est 996 + 128 = 1024 en mm).
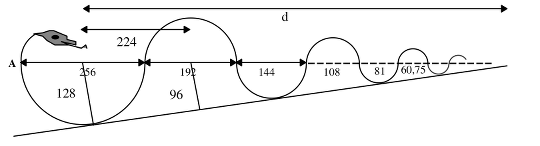
Quant à la longueur du serpent, la relation entre les diamètres et les longueurs des cercles, lorsqu'elle est perçue par les élèves, permet de passer de la progression géométrique 256, 192, 144, ... à la suite correspondante des mesures des longueurs des cercles : 128π + 96 π + 72 π + ... = 512 π, une valeur qui peut être approchée à 1600.
progression géométrique cercle, similitude, rapport, raison, limite, approximations, idée d’infini, convergence d’une série, Thales
sur 37 classes finalistes de 10 sections
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 8 | 11 (39%) | 14 (50%) | 1 (4%) | 2 (7%) | 0 (0%) | 28 | 0.79 |
| Cat 9 | 3 (27%) | 5 (45%) | 1 (9%) | 0 (0%) | 2 (18%) | 11 | 1.36 |
| Total | 14 (36%) | 19 (49%) | 2 (5%) | 2 (5%) | 2 (5%) | 39 | 0.95 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Selon les critères déterminés lors de l’analyse a priori :
Ces résultats sont établis sur un nombre limité de classes. Ils ont cependant été confirmés par une analyse plus approfondie en "Finale des finales" où ont été analysées les copies des classes "gagnantes" des 21 sections participant au 13e RMT, avec des moyennes des points inférieures à 1 dans les deux catégories concernées.
Dans de nombreuse copies, le rapport constant 4/3 est reconnu et appliqué (le plus souvent écrit sous forme décimale). Cependant, en général, les procédures n'ont pas permis de résoudre complètement le problème en raison, notamment, de la difficulté prévisible à imaginer un processus à l’infini de la queue du serpent. En revanche, les données selon lesquelles les diamètres des demi-cercles diminuent selon un rapport constant, ont permis à une partie de groupes d'élèves d'arriver à une réponse non loin de 1024, en ce qui concerne la distance entre le cou et la fin de la queue de serpent. Dans ce cas, cependant, un diamètre nul (par exemple 0,0075 assimilé à 0) était généralement supposé, à la fin du processus de division. Cette interruption du processus d'addition est souvent associée à la réponse sur le nombre de demi-cercles visibles, qui est identifié par le nombre fini d'additifs considérés, comme souligné dans la copie de catégorie 8 suivante :
En considérant que le rapport constant entre les différents diamètres est de 4/3, nous avons continué la division par ce nombre jusqu'à atteindre un nombre approximativement égal à 0. Nous avons obtenu : 256 mm; 192; 144; 108; 81; 60,75; 45,56; 34,17; 25,62; 19,22; 14,41; 10,81; 8.10; 6,08; 4,36; 3,48; 2,56; 1,92; 1,44; 1,02; 0,81; 0,60; 0,45; 0,34; 0,25; 0,19; 0,14; 0,10; 0, 02; 0,06; 0,04; 0,03; 0,02; 0,01; 0,00 (qui ne doit pas être compté comme un diamètre) qui additionnés tous ensemble donnent 1023,82 mm. Autrement dit, la distance entre le cou et la queue du serpent. Les cercles, en tout, sont 34 (nombre que nous avons obtenu en comptant les diamètres) et le serpent ne voit pas 28-29.
La relation entre les diamètres des cercles est aussi le protagoniste d'une "extrapolation subjective" d'un groupe d'élèves qui voit dans le nombre illimité de chiffres du nombre périodique, l'infinité de cercles, en mettant en évidence une confusion entre des aspects non liés entre eux.
Nous sommes arrivés à la conclusion que le rapport entre une circonférence et l'autre est 4/3 (256 • 4/3 = 192, 192 • 4/3 = 144). En continuant avec cette division les nombres diminuent toujours mais n'atteignent jamais zéro parce que le rapport entre les nombres est 4/3 qui est un nombre décimal illimité, périodique, simple. Donc les circonférences qu'il ne voit pas sont infinies.
Ce problème, qui, comme indiqué plus haut, va de la géométrie - avec la longueur du cercle, le théorème de Thales, la similitude - à l'arithmétique - avec les successions, le calcul de la somme des termes d'une progression géométrique - ainsi qu'une approche de l'idée de l'infini en mathématiques, elle se prête bien à être utilisée en classe pour des activités constructives sur ces thèmes, qui peuvent également conduire à des débats intéressants.
En particulier, la question du nombre de demi-cercles est particulièrement intéressante au regard d'un débat entre, d'une part, les élèves qui estiment qu'ils sont en nombre fini et, d'autre part, les élèves qui, bien qu'informellement, utilisent des expressions telles que « autant que vous voulez », « des centaines ou des milliers », « une infinité ».
Quelles réflexions les élèves font-ils dans ce cas ? Est-il difficile d'accepter que la somme des additifs infinis ait un résultat fini ? D'un point de vue géométrique, le conflit entre les concepts « infini » et « limité » émerge : un espace limité peut-il contenir des éléments infinis (demi-cercles infinis) ?
En effet, là où le mathématicien voit une approche de l'infini, le zoologiste (et de nombreux élèves) sait bien que le serpent a un corps de longueur finie. Il s'agit donc d'abandonner les contraintes de la réalité physique pour passer à la fiction mathématique ou, à l'inverse, induire des réflexions sur le degré de signification de la réponse en termes réels. Par exemple, en classe, on pourrait se demander quelle mesure de diamètre, au plus, pourrait être considérée comme significative ou perceptible. Ce serait l'occasion d'ouvrir la voie aux premiers aspects du type infinitésimal.
Gruppo Zeroallazero (C. Bisso, S. Foglia, L. Grugnetti, A. Maffini, C. Marchini, M. Rapuano, A. Rizza, V. Vannucci, con l'apporto dell'ARMT) Il sogno di Cirillo e la sfida della tartaruga (Pitagora Editrice- 2009).
(c) ARMT, 2005-2024