
Banque de problèmes du RMT
gp26-fr
 |
Banque de problèmes du RMTgp26-fr |
|
Calculer le côté d’un carré dans lequel est dessinée une "bande" de 112 m2 en forme d’hexagone ayant un axe de symétrie sur une diagonale du carré, et dont les quatre côtés coïncidant avec les côtés du carré (dans les angles) mesurent 4 m.
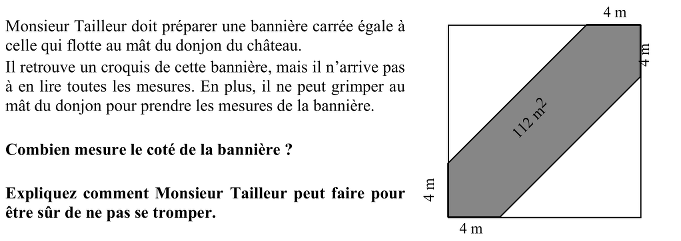
- Trouver les mesures des côtés de la bande colorée en se rendant compte qu’elle est formée d’un rectangle et de deux triangles qui sont chacun un demi-carré de 4m de côté.
L'aire du rectangle est ainsi de 112 – 16 = 96 m2, sa largeur est la diagonale d’un carré de 4m de côté : 4√2 et par conséquent, sa longueur est (en mètres) (96/4) √2 = 24/√2 puis trouver x d’après la relation x = d /√2 (en mètres) x = (24√2)/ √2 = 24 /2 = 12 et finalement en déduire la mesure du côté : 12 + 4 = 16 (mètres)
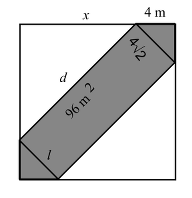
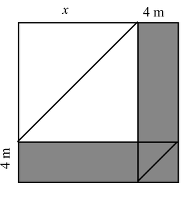
- Une autre méthode consiste à former un carré avec les deux triangles qui n’appartiennent pas à la bande et de transformer ainsi celle-ci en une figure d’aire équivalente, constituée d’un carré de 4 m de côté et deux rectangles de 4 m de largeur.
La longueur de chacun des deux rectangles se calcule ainsi immédiatement : 2(4x)+16=112 ->x=12
géométrie, triangle rectangle, similitude, diagonale, rapport, Pythagore, pavage, aire, côté
Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.
(c) ARMT, 2002-2024