
Banque de problèmes du RMT
gp6-fr
 |
Banque de problèmes du RMTgp6-fr |
|
Analyser une suite de carrés dont le côté d’un élément est la diagonale du précédent et calculer le côté du dixième, puis du centième carré de la suite.
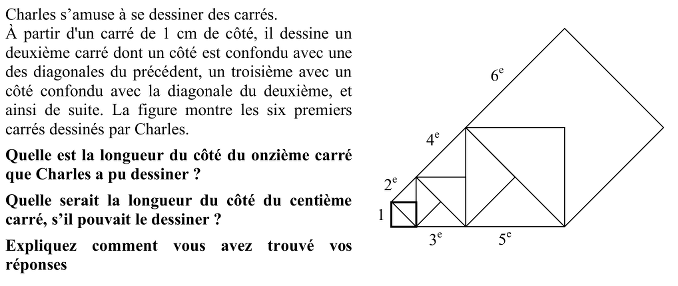
- Observer comment sont formés les carrés successif : le premier, le troisième, le cinquième ... , ceux d’ordre impair, sont disposés l’un à côté de l’autre « horizontalement » comme le deuxième, le quatrième ... ceux d’ordre pair, qui eux disposés l’un à côté de l’autre mais en « obliquement»
- Calculer la longueur de la diagonale du premier carré – qui est la longueur du côté du 2e carré et trouver $\sqrt{2}$ (en cm) par le théorème de Pythagore ou en se rappelant la relation entre côté et diagonale d’un carré : $d = c \sqrt{2}$ .
- Calculer la longueur du côté du troisième carré, soit par Pythagore, soit par la relation $d = c\sqrt{2}$ (qui conduit à $\sqrt{2} \times \sqrt{2} = 2$, soit par un quadrillage de la figure, dont l’unité est le premier carré, pour s’apercevoir que le troisième carré est constitué de 4 carrés de côté 1 cm et par conséquent a un côté qui est le double du premier carré : 2.
- Calculer (éventuellement) la longueur du côté du quatrième carré comme précédemment soit en multipliant le côté du précédent par $\sqrt{2}$, soit par quadrillage en constatant qu’il est composé de 8 carrés unités et que son côté est, en cm, $\sqrt{8} = 2 \sqrt{2}$, soit en doublant celui du deuxième carré.
- Organiser ensuite les résultats jusqu’au 11e carré et constater que son côté mesure 32, en cm. Par exemple :

- Se rendre compte que, pour aller au-delà du 11e carré, il devient nécessaire de faire un lien entre le numéro du carré et les exposants des mesures des côtés écrits sous forme de puissances de 2. (3e ligne dans l’exemple suivant) :

on y remarque que ces exposants valent la moitié du « numéro d’ordre du carré – 1 » : pour 11, (11 - 1)/2 = 5, pour 99, (99 - 1)/2 = 49.
- Obtenir ainsi la valeur du côté du 100e carré : $2^{49} \sqrt{2}$.
Ou : comprendre que les mesures des côtés des carrés d’ordre « impair » sont en progression géométrique de raison 2, avec 1 comme premier terme (et que le côté d’un carré « impair » de rang 2k + 1 est une puissance de 2 d’exposant k). Le côté du onzième carré, cinquième terme de la progression sera donc $2^5 = 32$.
- Comprendre, de même, que les mesures des côtés des carrés d’ordre « pair » sont en progression géométrique de raison 2, avec $\sqrt{2}$ (diagonale du carré de côté 1) comme premier terme (et que le côté d’un carré « pair » de rang 2k est le produit de $\sqrt{2}$ par une puissance de 2 d’exposant k - 1) et calculer la longueur du côté du centième carré : $\sqrt{2} \times 2^{49} \approx 7.960 \times 10^14$ cm, soit environ 7 milliards 960 millions de kilomètres (ce dernier calcul n’est pas attendu des élèves de niveaux 8, 9 ou 10 qui ne disposeraient pas d’une calculatrice scientifique).
géométrie, carré, similitude, diagonale, rapport, Pythagore, racine carrée, progression géométrique, raison, approximations, limite
Points attribués sur 698 classes de 21 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 8 | 219 (49%) | 76 (17%) | 100 (22%) | 19 (4%) | 31 (7%) | 445 | 1.03 |
| Cat 9 | 71 (49%) | 17 (12%) | 36 (25%) | 12 (8%) | 8 (6%) | 144 | 1.09 |
| Cat 10 | 46 (42%) | 14 (13%) | 26 (24%) | 8 (7%) | 15 (14%) | 109 | 1.38 |
| Total | 336 (48%) | 107 (15%) | 162 (23%) | 39 (6%) | 54 (8%) | 698 | 1.09 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Bisso C., Grugnetti L., Maffini C., Marchini C., Rapuano M., Speroni A., Vannucci V. e ARMT. (2011) ‘Alla ricerca del segmento perduto’. Bologna: Pitagora Editrice.
(c) ARMT, 2010-2024