I dieci punti

Identification

Rallye: 18.I.08 ; catégories: 5, 6, 7 ; domaine: GP
Familles:

• IF - Identificare figure
• IF/RC - Riconoscere e costruire figure elementari
• QUA - Lavorare su una quadrettatura
• QUA/GQ - Gestire poligoni su carta quadrettata

Envoyer une remarque ou une suggestion

Résumé

A partire da dieci punti su una griglia quadrettata, ricerca di gruppi di quattro punti che formano dei quadrilateri aventi le proprietà caratteristiche del rettangolo.

Enoncé

Tâche de résolution et savoirs mobilisés

Mobilizzare le competenze sul rettangolo: lati paralleli congruenti e lati perpendicolari, oppure diagonali della stessa lunghezza e che si tagliano nel loro punto medio.

Cercare coppie di segmenti paralleli e congruenti e verificare per ciascuna di tali coppie se esistono delle coppie di segmenti congruenti perpendicolari.

Organizzare un inventario sistematico, controllando in modo “visivo” il parallelismo e la congruenza nel fare riferimento alla quadrettatura.

• Ulteriori verifiche possono essere fatte con il ricorso a strumenti geometrici: squadretta (per gli angoli retti), riga e ancora squadretta (per il parallelismo), il compasso per la congruenza.
• La giustificazione del parallelismo e della congruenza dei lati può essere data nel considerare gli spostamenti verticali e orizzontali che permettono di passare lungo la quadrettatura da un vertice del rettangolo al vertice consecutivo (immaginando per esempio che ciascuno dei lati sia una diagonale di un rettangolo 6x7, formato sulle linee della quadrettatura).
• Riguardo alla perpendicolarità, si può fare appello alle rotazioni di un quarto di giro di diagonali di rettangoli le cui misure dei lati sono “scambiate” (per esempio, una diagonale di un rettangolo di 1 x 2 si ritrova, dopo una rotazione di un quarto di giro, come diagonale di un rettangolo isometrico di 2 x 1).

Notions mathématiques

proprietà del rettangolo

Résultats

18.I.08

Punteggi attribuiti su 1471 classi di 18 sezioni

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta e completa: disegno dell’unico rettangolo possibile, CHGE e risposta “Anna ha torto”; con spiegazione sul perché si è sicuri che si tratti di un rettangolo (i quattro angoli retti o altre condizioni necessarie e sufficienti (si veda più sopra). Non è sufficiente dire che i lati opposti sono paralleli e della stessa “lunghezza”.
• 3 punti: Risposta corretta, ma incompleta: disegno dell’unico rettangolo possibile e dichiarazione che è l’unico, ma senza dire perché si è sicuri che sia un rettangolo

    * oppure: disegno dell’unico rettangolo possibile, CHGE, con spiegazione del perché si è sicuri che si tratti di un rettangolo, ma senza dichiarazione che dica che non è possibile disegnarne altri
2 punti:  Disegno del rettangolo CHGE e la dichiarazione che Anna può disegnarne anche un altro confuso con il parallelogramma BJFD
1 punto:  Disegno del rettangolo CHGE con altri parallelogrammi 
    * oppure solo il parallelogramma BJFD 
0 punto:  Incomprensione del problema

Procédures, obstacles et erreurs relevés

Le procedure di ricerca delle coppie di segmenti paralleli e congruenti sono dapprima di tipo “visivo”, poi analitiche per esempio tramite un controllo con il ricorso a strumenti. Si trova così che non ci sono coppie di segmenti paralleli alle righe della griglia e che ci sono solo 4 coppie da prendere in considerazione: BD e JF, BJ e DF, CE e HC, CH e EG.

Si arriva così a due parallelogrammi BJFD e CHGE (due coppie di lati paralleli congruenti).

Per controllare l’angolo retto si può utilizzare la squadretta o il goniometro, o ricorrere ad un’analisi fine delle posizioni dei lati in rapporto alle righe della griglia. Per esempio, per BJFD, si può osservare che i lati BJ e DF seguono nodi della quadrettatura, cosa che non succede per i lati BD e JF. E così si ottiene un solo rettangolo CHGE.

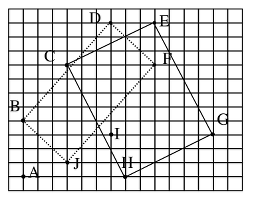
La tabella dei risultati mostra che solo un quarto (punteggio 3 e 4) degli allievi di categoria 5 e 6 danno CHGE come unico rettangolo, e che la metà (punteggi 1 e 2) dicono che i due parallelogrammi sono rettangoli o trovano un altro rettangolo ancora.

Ci sono dunque seri ostacoli a proposito del riconoscimento di rettangoli o della distinzione tra parallelogrammi rettangoli e parallelogrammi non rettangoli.

• Un primo ostacolo è verosimilmente di natura ontogenetica, legato allo sviluppo di rappresentazioni dell’allievo. I modelli di riferimento per il rettangolo sono in generale oggetti a tre dimensioni (tavoli, porte, facce di un parallelepipedo rettangolo, ...; la loro proiezione su un piano (ombra, immagine formata sulla retina) conservano solo il parallelismo dei lati e non gli angoli retti; sono dei parallelogrammi. Il bambino deve passare dall’immagine, deformata dalla proiezione, all’oggetto per ricostruire una figura del piano che tenga conto della perpendicolarità.
• Un secondo ostacolo può essere originato da abitudini scolastiche dove il rettangolo è quasi sempre presentato con i lati paralleli ai bordi del foglio.
• Un terzo ostacolo, nel caso dei due parallelogrammi “candidati” viene dall’accontentarsi di una prima impressione visiva che non è sufficiente a determinare lo statuto di rettangolo, in particolare per ciò che riguarda gli angoli retti.

Exploitations didactiques

Questo problema si presta bene ad una messa in comune e ad un dibattito relativo alle soluzioni prospettate dagli allievi, probabilmente diverse; tale dibattito farà sorgere la necessità di superare l’impressione visiva per andare verso le proprietà del rettangolo, con l’uso degli strumenti tradizionali e della quadrettatura. Questa attività non andrebbe svolta a partire dall’ingiunzione del genere “prendete la squadretta”, dove l’iniziativa del collegare lo strumento alla figura viene dall’esterno, ma a partire da un’idea concepita in seno al gruppo di allievi.

Ma si può anche andare più lontano, verso una giustificazione tramite le “componenti” orizzontale e verticale dei segmenti considerati come diagonali di rettangoli. Si tratta di una “iniziazione” naturale al concetto di vettore e delle sue componenti.

Pour aller plus loin

Il problema I dieci punti fa parte di una serie di problemi “isomorfi”, basati sulla conservazione di lunghezze e sul ruolo essenziale dell’angolo retto.

• I dieci punti (18.I.8 – 5,6,7): individuare e costruire un rettangolo a partire da punti su una griglia quadrettata
• Il tavolo da spostare: Individuare i vertici “mancanti” di rettangoli su una griglia quadrata a partire da uno o due vertici dati.
• Sul muro della scuola(I) (18.II.6 – 4, 5) e Sul muro della scuola (II) (18.II.13 – 6, 7, 8): distinguere il rettangolo dal parallelogramma non rettangolo tramite le loro proprietà caratteristiche
• Il ritaglio di triangoli (19.II.13): Individuare triangoli isosceli con due dei lati congruenti ad un segmento dato su una griglia quadrata

L’articolo “rettangolo...non così evidente”, pubblicato sul n. 1 de La Gazzetta di Transalpino (sul sito www.armtint.org) tratta l’argomento con una certa ampiezza.

Bibliographie

Anselmo B., Bisso C., Grugnetti L.: 2011 ‘Il rettangolo...non così evidente/ Le rectangle...pas si évident”, in La Gazzetta di Transalpino/La Gazette de Transalpie, n. 1, 7-41, http://www.armtint.org/fr/le-gazzette-di-transalpino/numero-1/viewcategory/12-gazzetta-n-1-articoli-gazette-n-1-articles

Crociani C., Doretti L., Grugnetti L. : 2012 ‘Difficoltà nel confronto di lunghezze/Difficultés dans la comparaison de longueurs’, in La Gazzetta di Transalpino/La Gazette de Transalpie, n. 2, 71-98, http://www.armtint.org/fr/le-gazzette-di-transalpino/numero-2/viewcategory/11-gazzetta-n-2-articoli-gazette-n-2-articles