
Banque de problèmes du RMT
gp91-fr
 |
Banque de problèmes du RMTgp91-fr |
|
Trouver la longueur du périmètre d’une figure composée de deux arcs de cercles de 3 et 15 cm de rayons et de deux segments tangents aux deux cercles, dans le contexte de deux roues reliées par une courroie de transmission. (On a dessiné sur la figure l’angle de 60 degrés formé par le segment reliant les centres des deux cercles et le rayon du grand cercle menant au point de contact d’un des segments tangents).
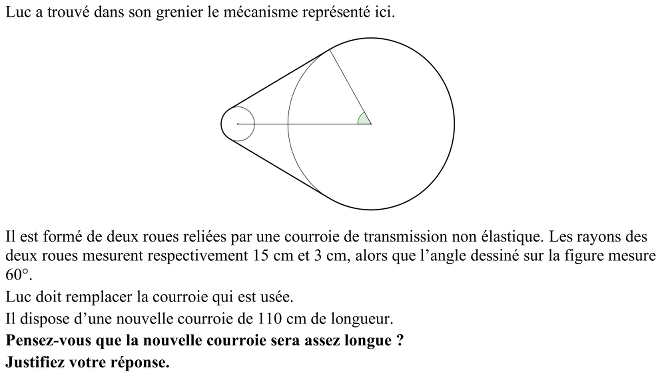
- Imaginer le dispositif de la courroie et des deux cylindres, puis passer à la figure géométrique « courroie » composée de deux segments et de deux arcs de cercle. Analyser cette figure et la compléter afin d’obtenir des figures à propos desquelles on dispose de connaissances métriques : triangles, rectangles, parallélogrammes, trapèzes, … Par exemple : segment parallèle à l’un des côtés de la courroie dont une extrémité est le centre du petit cercle, prolongements des deux segments et de la courroie et du segment reliant les deux centres jusqu’à leur point d’intersection, …
- Reconnaître dans ces nouvelles figures les angles droits, les isométries, symétries, parallélismes, homothéties. Distinguer les mesures de longueur (3, 15) et d’angles (60, 90) connues, de celles qu’on peut déduire facilement des autres (longueurs des arcs) et de celles qui restent provisoirement inconnues (dont la longueur des deux segments).
- Poser une équation permettant d’obtenir la longueur des deux segments de la courroie et calculer sa longueur.
- Savoirs mobilisés : tangente, point de contact, perpendicularité de la tangente et du rayon déterminé par le centre et le point de contact, détermination de la longueur d’un arc en fonction de son angle et du rayon, relation de Pythagore, propriétés du demi-triangle équilatéral, théorème de Thalès, homothétie, similitude, résolution d’une équation du premier degré, arrondis de π ou de √3.
Ces savoirs dépendent évidemment des figures choisies pour les mises en relation des longueurs à déterminer. (Voir rubrique procédures, obstacles et erreurs relevés)
géométrie, cercle, longueur, arc, tangente, rayon, homothétie, angle, périmètre, trapèze, triangle, Pythagore, similitude
Points attribués, sur 289 copies de 10 sections
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 9 | 107 (66%) | 37 (23%) | 9 (6%) | 3 (2%) | 6 (4%) | 162 | 0.54 |
| Cat 10 | 71 (56%) | 28 (22%) | 13 (10%) | 4 (3%) | 11 (9%) | 127 | 0.87 |
| Total | 178 (62%) | 65 (22%) | 22 (8%) | 7 (2%) | 17 (6%) | 289 | 0.69 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
Selon les critères déterminés lors de l’analyse a priori :
Le problème s'est révélé difficile, surtout pour le calcul de la longueur des segments de tangentes BC et KH communes aux deux cercles et pour la reconnaissance de l'arc de cercle BK du petit cercle. Ces difficultés ont entraîné l'abandon des calculs, dans la plupart des cas, après avoir déterminé la longueur de l'arc HC. Ceux qui ont poursuivi ont commis l'une ou l'autre des erreurs:
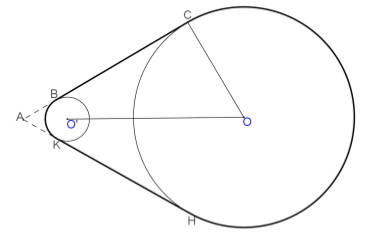
a. ont considéré l’arc BK come un demi-cercle,
b. ont substitué à la somme BC+BK+KH la somme AC+AH et par conséquent effectué une approximation par excès.
La question du problème et la nécessité de donner une approximation de la longueur pour la comparer avec les 110 cm de la donnée incite à utiliser des mesures approximatives dès le début de la résolution. La présence d'écritures symboliques comme π ou √3 est très rare, même dans les résolutions correctes. On pense que ce choix est conscient, au moins dans quelques cas.
On observe dans quelques copies analysées la tentative de tirer des informations de la figure comme, par exemple de “voir” deux carrés, l'un dont le côté est le rayon du grand cercle et l'autre dont le côté est le diamètre du petit cercle (on commet ainsi une "petite" erreur étant donné que le segment BC mesurerait 21 plutôt que 20,78)
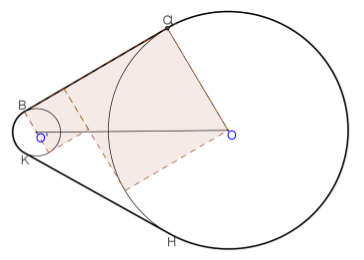
La courroie de Luc est un « beau » problème du point de vue de l’enseignant mais évidemment, au vu des résultats obtenus, « beaucoup trop difficile » pour des élèves de 15 à 16 ans dans les conditions de passation des épreuves du RMT.
Chacune des connaissances nécessaires à la résolution figure dans les programmes de géométrie aux degrés se situant à l’articulation entre le secondaire inférieur et le secondaire supérieur. L’analyse a posteriori du problème montre que la gestion combinée et coordonnée des démonstrations et applications de théorèmes n'est généralement pas encore possible à cet âge (elle le sera peut-être en fin de secondaire supérieur). Cependant, quelques groupe d'élèves (bien que peu nombreux) ont résolu correctement le problème par des procédures justifiées, étape par étape.
Malgré toutes ces réserves, le problème montre l’intérêt de la synthèse des connaissances géométriques et d’une démarche scientifique faisant appel à une grande variété de savoirs. Pour l’exploiter en classe, il faut donc que le maître en organise une gestion didactique tenant compte de sa complexité : mises en commun successives à différents niveaux : appropriation du dispositif, analyse de la figure « courroie », découvertes de figures accessoires internes, … tout en conservant l’énoncé original et évitant les « petites marches » où tout est à la charge de l’enseignant.
(c) ARMT, 2014-2024