Navi - bel affichage d'une fiche

Tous en file (II)

Identification

Rallye: 30.I.11 ; catégories: 5, 6, 7 ; domaine: LR
Familles:

Résumé

Trouver les différentes permutations dans une suite ordonnée de 14 objets de trois couleurs avec des conditions données.

Enoncé

Tâche de résolution et savoirs mobilisés

Analyse a priori:

À la lecture des conditions données, placer les maillots gris à chaque extrémité, puis deux maillots rouges qui suivent et un maillot bleu (puisqu’il ne peut pas avoir plus de deux maillots d’une même couleur qui se suivent). Il reste à déterminer les couleurs de six maillots au centre de la file : trois bleus et trois rouges.

La tâche est de trouver les permutations différentes de ces six objets par une méthode permettant d’être certain de ne pas en oublier ni de reprendre plusieurs fois la même. Il y a évidemment de nombreuses manières d’organiser l’inventaire, dont celle qui consiste à procéder par essais au hasard et contrôles.

-L’inventaire suivant des dix solutions est issu d’une procédure dans laquelle on donne la priorité à B sur R dans le sens de la lecture :

Notions mathématiques

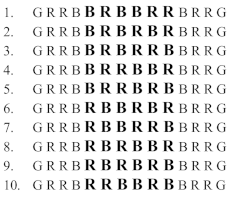
combinatoire, combinaison, arrangement, permutation

Résultats

30.I.11

Points attribués sur 3332 classes de 19 sections:

Catégorie	0	1	2	3	4	Nb. de classes	Moyenne
Cat 5	505 (55%)	203 (22%)	143 (15%)	63 (7%)	9 (1%)	923	0.77
Cat 6	705 (56%)	237 (19%)	211 (17%)	89 (7%)	18 (1%)	1260	0.79
Cat 7	497 (43%)	258 (22%)	249 (22%)	118 (10%)	27 (2%)	1149	1.06
Total	1707 (51%)	698 (21%)	603 (18%)	270 (8%)	54 (2%)	3332	0.88
Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème.

Selon les critères déterminés lors de l’analyse a priori :

4 points: Réponse correcte (dessin des 10 possibilités correctes)
3 points: Réponse avec 1 ou 2 erreurs (oubli, doublon ou non-respect d’une condition)
2 points: Réponse avec 3 ou 4 erreurs
1 point: Réponse avec 5 ou 6 erreurs
0 point: Incompréhension du problème
ou réponse avec plus de 6 erreurs

Procédures, obstacles et erreurs relevés

Les résultats montrent que le problème est difficile pour des élèves de toutes les catégories

Il s'agit de combinatoire, qui exige une organisation systématique des files possibles pour trouver le nombre de « permutations » respectant les trois conditions de l'énoncé.

Voir les autres problèmes de la famille:

Chercher des arrangements ou des combinaisons du domaine Logique et raisonnement

Les desserts de Samia (27.I.04), Monsieur Charles (26.I.06), Les cubes de Nicolas (26.II.10) ainsique la version I du problème Tous en file (I) (30.I.05)

Banque de problèmes du RMT