
Banca di problemi del RMT
sd248-it
 |
Banca di problemi del RMTsd248-it |
|
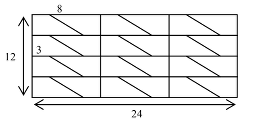
Ricoprire un rettangolo il cui lato misura 12 cm, con 24 trapezi rettangoli identici di perimetro 16 cm e in cui tutti i lati misurano un numero intero di centimetri tutti diversi fra loro.

- Capire che occorre individuare com’è fatto il trapezio rettangolo per risalire al rettangolo
- Osservare che un trapezio rettangolo è sempre scomponibile in un rettangolo ed in un triangolo rettangolo. Poiché i lati del trapezio hanno misure date da numeri interi e il perimetro è di 16 cm, dedurre che le misure dei lati del triangolo rettangolo devono necessariamente essere espresse dalla “più piccola” terna pitagorica: 3, 4, 5. (le successive: 6, 8, 10 , 9, 12, 15 oppure 5, 12, 13 portano ad una somma maggiore di 16).
- Determinare la base minore del trapezio: a partire dal perimetro del triangolo, 3 + 4 + 5 = 12, constatare che bisogna completare la figura con un rettangolo di 2 cm di larghezza per ottenere un trapezio di perimetro 16 cm. Concludere che si hanno due possibili trapezi: (misure: 2 ; 3 ; 6 ; 5 e 2 ; 4 ; 5 ; 5) e che bisogna eliminare il secondo perché le misure dei lati del trapezio devono essere differenti:

- Osservare che, unendo due trapezi uguali lungo il loro lato obliquo, si ottiene un rettangolo di dimensioni 3 x 8
- A partire dal segmento di 12 cm, cominciare a disporre trapezi rettangoli dello stesso tipo (si può lavorare anche con rettangoli unione di due trapezi) e verificare che c’è una sola isposizione, nella quale le basi sono perpendicolari ai segmenti di 12 cm: dedurne che il rettangolo che contiene i 24 trapezi ha una lunghezza di 24 cm.
rettangolo, trapezio rettangolo, pavimentazione, perimetro, area, teorema di Pitagora, scomposizione di un numero, somma, prodotto, terne pitagoriche
I risultati non sono stati salvati o non sono ancora disponibili.
(c) ARMT, 2005-2024