Navi - bel affichage d'une fiche

Etoiles

Rallye: 06.F.14 ; catégorie: 8 ; domaine: GP
Familles:

Déterminer le nombre de polygones étoilés réguliers de 15 sommets que l'on obtient en les reliant d'un seul trait, sans lever le crayon.

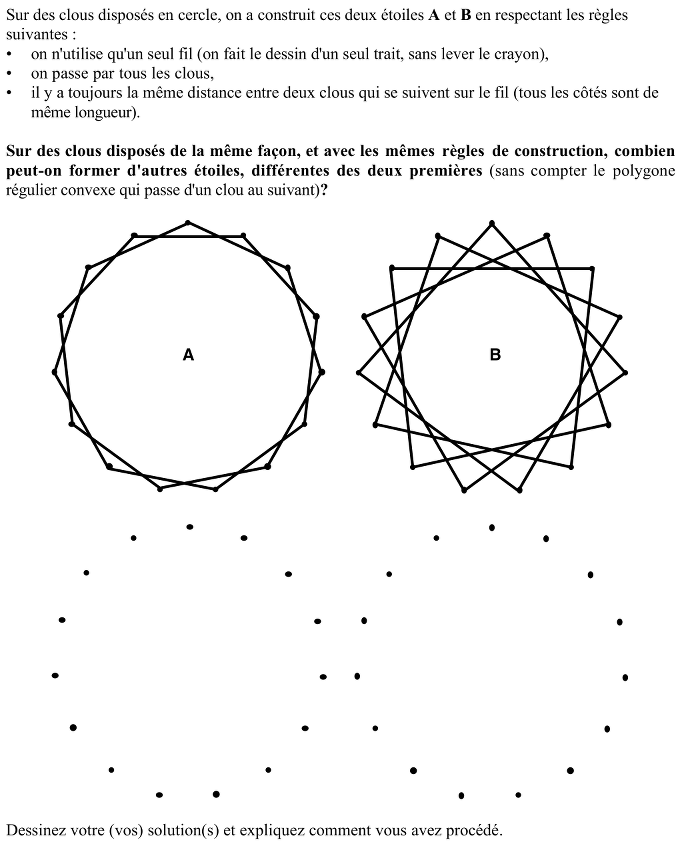
Analyse a priori de la tâche :

- Observer les figures A et B et comprendre leur construction

- Rechercher d'autres polygones réguliers étoilés de 15 sommets, par essais successifs, ou construire un raisonnement sur les numéros des sommets :

de 2 en 2 : 0 - 2 - 4 - .....14 - 1 - 3 - ... 15 ≡ 0 (figure A, comme de 13 en 13)
de 3 en 3 on ne passe que par 0 - 3 - 6 - 9 - 12 - 15 ≡ 0 (comme de 12 en 12), ce n'est pas une solution
de 4 en 4 : 0 - 4 - 8 - 12 - 1 - 5 - 9 - 13 - 2 - 6 - 10 - 14 - 3 - 7 - 11 - 15 ≡ 0 (figure B, comme de 11 en 11)
de 5 en 5 on ne passe que par 0 - 5 - 10 - 15 ≡ 0 (comme de 10 en 10), ce n'est pas une solution
de 6 en 6 on ne passe que par 0 - 6 - 12 - 3 - 8 - 15 ≡ 0 (comme de 9 en 9), ce n'est pas une solution
de 7 en 7 : 0 - 7 - 14 - 6 - 13 - 2 - 9 - 1 - 8 - 15 ≡ 0 C'est le troisième et dernier polygone qu'on peut tracer en un seul coup de crayon. (idem que de 8 en 8)

dessin, polygone régulier étoilé, diviseur, multiple, calcul modulo 15

Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.