
Banca di problemi del RMT
ud193-it
 |
Banca di problemi del RMTud193-it |
|
Envoyer une remarque ou une suggestion
Confrontare le aree di due poligoni (di 8 e 12 lati) disegnati su una quadrettatura, con i cui vertici posti su intersezioni della quadrettatura stessa e i lati che si trovano sui lati o sulle diagonali dei quadretti della quadrettatura, in un contesto di foglie da ritagliare.
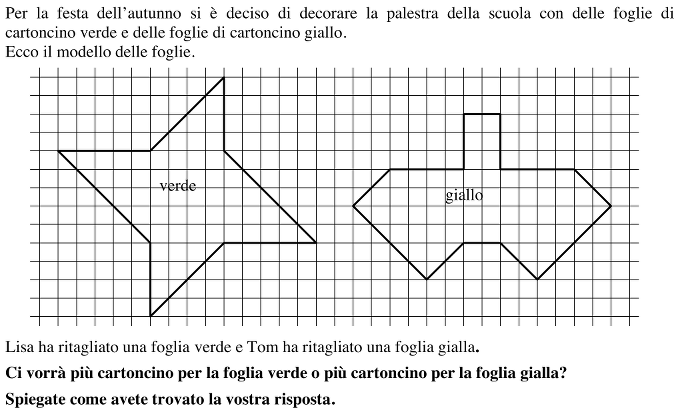
Analisi a priori
- Comprendere che è necessario confrontare le aree delle due figure
- Contare i quadretti e i semi-quadretti di ciascuna figura uno a uno (metodo soggetto ad errori di conteggio), poi effettuare gli scambi necessari per poterli contare secondo un’unità di misura comune: in quadretti (o semi-quadretti), 61 (122) per la figura verde e 62 (124) per la gialla. (Nel caso in cui si contassero i “pezzetti”, senza tener conto delle loro aree rispettive, si otterrebbero 70 pezzi per la figura verde e 70 per quella gialla).
- Oppure: con una scomposizione opportuna delle figure in rettangoli, quadrati e triangoli, rendersi conto che i triangoli sono metà di quadrati.
- Ricostruire quindi i quadrati “interi” per contarne i quadratini. Per esempio, osservare che la figura verde è composta da due triangoli che costituiscono un quadrato di 4 x 4, da due triangoli che costituiscono un quadrato di 5 x 5 e da un rettangolo di 5 x 4, per un’area di 16 + 25 + 20 = 61 (in quadretti). Nello stesso modo, si possono raggruppare le parti della figura gialla in quattro quadrati di 2 x 2 e due rettangoli di 4 x 10 e 2 x 3 per ottenere un’area di 40 + 6 + 4 x 4 = 62 (in quadretti).
Oppure: procedere ritagliando una delle due foglie per ricoprire l’altra e constatare che manca (o avanza) un pezzo e concludere che la foglia gialla ha un’area maggiore.
poligono, quadrettatura, area, equivalenza, triangolo, rettangolo, quadrato, trapezio, scomposizione, ricomposizione, transformazione geometrica, unità d’area
Su 1352 classes di 21 sezioni partecipanti alla prova
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 3 | 148 (47%) | 60 (19%) | 32 (10%) | 34 (11%) | 44 (14%) | 318 | 1.26 |
| Cat 4 | 148 (30%) | 60 (12%) | 57 (12%) | 93 (19%) | 131 (27%) | 489 | 2 |
| Cat 5 | 119 (22%) | 50 (9%) | 74 (14%) | 105 (19%) | 197 (36%) | 545 | 2.39 |
| Totale | 415 (31%) | 170 (13%) | 163 (12%) | 232 (17%) | 372 (28%) | 1352 | 1.98 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Una prima analisi a posteriori, parziale, è stata presentata nell’articolo di de Lucia Grugnetti Analisi a priori, analisi a posteriori, oltre il percorso circolare pubblicato sulla Gazzetta di Transalpino n. 4, agosto 2025 pp. 75-94. Di cui è riportato qui qualche passaggio:
Come si è visto nella rubrica “attribuzione dei punteggi”, il punteggio 0 contempla il ”ricorso al perimetro per confrontare le figure o conteggio dei pezzi senza tener conto della loro area”.
L’analisi svolta dai membri del gruppo geometria, nelle loro sezioni di appartenenza e ampiamente riportata in Anselmo et al. (2011), mostra che in effetti, il punteggio 0 è sempre stato attribuito a causa dei due tipi di difficoltà ricordati e non per incomprensione del problema.
le percentuali (per il punteggio 0) vanno decrescendo nel passare dalla categoria 3 (49%, su 290 elaborati) alla 4 (30%, su 489 elaborati) fino alla 5 (22% su 545 elaborati).
... pour cette attribution, les pourcentages décroissent en passant de la catégorie 3, (49%, sur 290 copies) à la 4 (30%, sur 489 copies) et enfin à la 5 (22% sur 545 copies).
Questi risultati indicano comunque che ancora in categoria 5 gli allievi incontrano gli ostacoli e le difficoltà più sopra citate, anche se in misura minore. Sarà importante proporre altri problemi similari al fine di verificare ancora l’esistenza delle difficoltà in oggetto, ma anche per cercare di capire a quale età vengano superate.
Il percorso che porta dall’analisi a priori all’analisi posteriori, per tornare a quella a priori, da circolare diventa in qualche modo a spirale, una spirale di percorsi circolari successivi.
In questa sede l’attenzione è posta sulle difficoltà e gli ostacoli, ma è importante ricordare che le analisi a posteriori dei problemi del RMT prendono in considerazione tutta la gamma delle risposte e delle spiegazioni e spesso succede che ci si renda conto di quanti tipi di soluzioni gli allievi prospettino che non erano state “pensate” dagli adulti nella preparazione dell’analisi del compito.
Un bell’esempio è il seguente.
Esempio 1

Analisi a posteriori per la preparazione della sperimentazione in classe (2025).
L'esame di un campione di 142 elaborati della sezione SI rivela:
a) 20%: risposte 62 (giallo) 61 (verde), conteggio dettagliato (o errore di conteggio) o talvolta scomposizione e ricomposizione delle figure in triangoli, rettangoli e quadrati, o confronto per taglio e sovrapposizione (come nell'esempio 1).
Exempio 2 (Categoria 5)
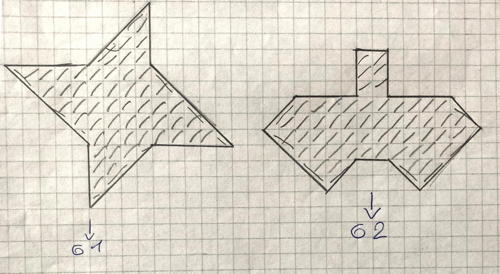
Ci sono effettivamente 61 e 62 trattini su queste figure, alcune più lunghe di altre perché coprono due triangoli, che vengono contati come 1 trattino o quadratino intero, con la padronanza del rapporto 2 a 1.
b) 15%: risposte (il più delle volte "gialle") senza alcuna spiegazione se non "abbiamo contato i quadrati".
c) 10%: risposta 70 (giallo) 70 (verde), (o errore di conteggio) corrispondente al numero totale di quadratini interi e triangoli (mezzi quadrati).
d) 20%: risposte tra 30 e 36 corrispondenti al conteggio dei quadrati disposti sul perimetro o dei lati e delle diagonali dei quadrati perimetrali.
Esempio 3 (Categoria 4)
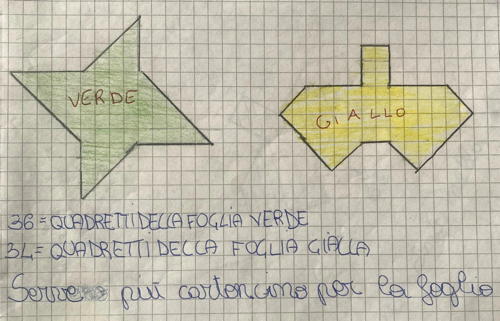
Abbiamo contato il contorno delle 2 foglie. All'inizio ci tornavano uguale ma poi contando meglio abbiamo capito che le foglie verde avevano bisogno di 36 quadretti et le foglie gialle di 34.
e) 35%: altre risposte come "incomprensione del problema" o misurazioni in cm e applicazione errata delle formule per l'area, o errori nel disegno.
Esempio 4 (Categoria 5)
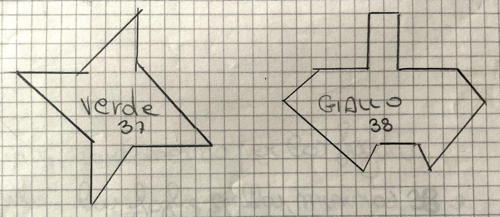
Esempio 5 (Categoria 4)
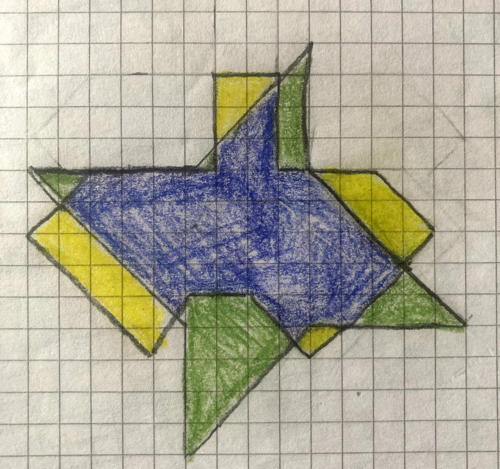
Questi allievi non gestiscono convenientemente il disegno su una quadrettatura, come nel caso dell'esempio seguente dove lavorano per "sovrapposizione".
Questi sono i tipi di risposte che l'insegnante vedrà probabilmente emergere quando farà a messa in comune dei risultati.
La fase più delicata per l'insegnante è quella che consiste nel gestire la discussione collettiva dei risultati senza voler "insegnare" perché la parola viene data agli allievi i quali devono rendersi conto che le risposte 61 e 62 sono corrette, che possono essere spiegate con il conteggio uno a uno per scomposizione, poi per ricomposizione o sovrapposizione”. Gli allievi, inoltre, con la discussione, devono poter essere in grado di spiegare perché le risposte di tipo c (con aggiunte di unità diverse), di tipo d (confusione di area e perimetro) o altri errori, non sono corrette.
L'insegnante dovrebbe osservare e porre domande per aiutare gli allievi a chiarire le loro argomentazioni. Ogni dettaglio può essere preso in considerazione a seconda delle competenze da rafforzare (vedere la rubrica precedente sui saperi mobilizzati).
A proposito dell'esempio 3 riportato più sopra, dei fogli colorati, chiedere il significato della parola "contorno", quindi di mostrare da dove provengono i 34 e 36 "quadretti" per far constatare che si tratta di 34 e 36 "lati" o "diagonali" dei quadretti, quindi chiedere nuovamente agli autori di questo elaborato se questi "lati" e "diagonali" hanno la stessa lunghezza.
Al termine della messa in comune, si tratta di organizzare il lavoro individuale in modo che ogni allievo tragga beneficio da quanto discusso collettivamente, perché, ovviamente, le risposte 61 e 62, sebbene ben spiegate, sono lungi dall'essere sufficienti dal punto di vista dei saperi da ricostruire o consolidare.
Ecco un programma minimo per la fase di "studio individuale", che dovrebbe figurare nel quaderno di ogni allievo:
1. disegnare le due foglie su carta quadrettata e colorale (area, disegno su quadrettatura)
2. descrivere le due figure (poligoni, numero di lati e vertici, ecc.)
3. determinare quale delle due figure ha il perimetro maggiore (misura di lunghezza, unità comune, confronto di lunghezza, approssimazioni, ecc.)
4. determinare l'area di ciascuna figura, in quadrati della quadrettatura, in semi-quadrati triangolari, eventualmente in cm² nel caso di una quadrettatura i cui quadratini abbiano lato 5 mm (misura dell'area, unità comune, rapporto tra unità comuni)
5. se possibile, passaggio a una procedura più elaborata che vada oltre il conteggio uno a uno, ad esempio per scomposizione in triangoli e poi ricomposizione in quadrati (ingresso nell'aritmetica, uso della moltiplicazione o dell'addizione ripetuta, scomposizione e ricomposizione "additiva" di figure geometriche).
Esempio 6 (Categoria 4)
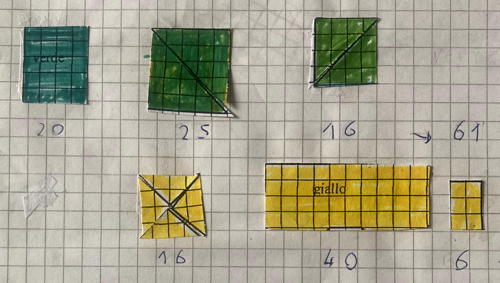
Le scritture 20, 25, 16 -> 61 e 16, 40, 6 -> 62 (troncate nella riproduzione) mostrano che gli allievi sono andati oltre il conteggio uno a uno per entrare nell'aritmetica dopo aver scomposto le foglie per ricomporle in rettangoli.
Esempi di attività per un percorso didattico con la classe
Da sperimentare in classe, secondo le modalità stabilite dall'insegnante; con invio descrizione e commenti per mostrare la rilevanza dell'attività ai fini dell'acquisizione di saperi (indicati in corsivo).
a) Esprimere le proprietà di simmetria delle due figure (e di altre) per ritaglio, piegatura e rotazione.
La foglia gialla ha un asse di simmetria, la foglia verde ha un centro di simmetria o un centro di rotazione di mezzo giro, ecc.
b) Allineare i lati delle due foglie disegnandoli consecutivamente e distinguendo i lati sulle linee della quadrettatura dei segmenti obliqui;
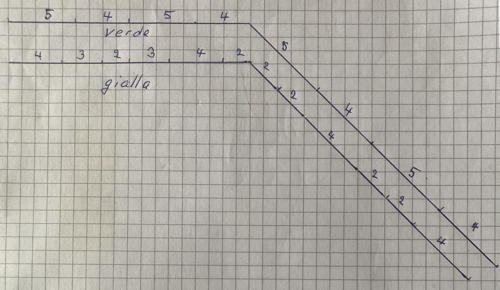
Poi, con l’aiuto del compasso, riportare le parti “oblique” sulle righe della quadrettatura per ottenere i due “perimetri” di lunghezze visibilmente differenti.
Rendersi conto che le diagonali dei quadretti della quadrettatura sono più lunghe dei lati dei quadretti
c) Cercare altri poligoni di 62 quadretti (su una quadrettatura con quadratini interi o mezzi quadratini), incluso quello con il perimetro più corto e quello più lungo!!
Rendersi conto che ci sono molti poligoni con la stessa area (62 quadratini) e che i loro perimetri possono essere molto diversi.
d) Molti altri problemi riguardano confronti di aree, su quadrettature, reticoli o tramite altre scomposizioni in unità di area.
La rosa di Giulia I (15.II.04), La rosa di Giulia II (15.II.07)
Rettangoli di carta quadrettata (I) (ral. 29.I.04) Rettangoli di carta quadrettata (II) (ral. 29.I.08)
Il giardino del signor Torquato (08.I.06)
Grugnetti, Lucia (2015). Analisi a priori, analisi a posteriori, oltre il percorso circolare. Gazetta di Transalpino no 4, agosto 2015, pp. 75-94
Anselmo, Bernard. Bisso, Clara, Grugnetti, Lucia (A nome del Gruppo geometria piana: Bernard Anselmo, Chiara Badiali, Silvana Bisogni, Clara Bisso, Jean-Louis Billody, Fabio Brunelli, Florence Falguères, Lucia Grugnetti, Elisabetta Mari, André Nguyen, Letizia Pucci, Michele Rapuano, Elsa Renna, Samia Mehaddene, M. Francesca Tanda, Agnese Tomasini, Donata Tardio, con la collaborazione di Anna Maria D’Andrea e Francesca Ricci). **Il rettangolo ... non così evidente**. In Gazette de Transalpie no 1, 2011, pp. 7-11
Grugnetti, L. Jaquet, F. Problemi, che passione! (Lugo 14 maggio 2025) In Gazzetta della BPrmt à paraître.