
Banca di problemi del RMT
ud237-it
 |
Banca di problemi del RMTud237-it |
|
Envoyer une remarque ou une suggestion
Confrontare l'area di due parti di un quadrato.
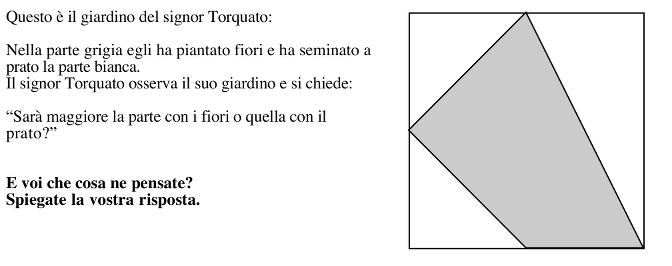
- Geometria: figure congruenti, scomposizione e ricomposizione di figure, equivalenza
Analisi del compito
- Intuire che la parte grigia e quella bianca sono formate dagli stessi “pezzi”
- Verificarlo ritagliando i pezzi
- Dedurre che la parte con i fiori ha la stessa estensione di quella seminata a prato
Per questo problema non esistono risultati “statistici” dei primi anni del Rally Matematico Transalpino, ma un'analisi dettagliata delle risposte di un centinaio di classi, riassunte nel successivo paragrafo “Procedure, ostacoli ed errori rilevati” e nell'articolo “Conflitto area-perimetro” riportato in bibliografia.
I risultati qui presentati sono quelli delle classi del parmense e della Svizzera romanda: 39 classi di categoria 3 (rispettivamente 8 e 31) e 70 classi di categoria 4 (14 e 56).
La tabella seguente presenta le diverse procedure osservate (prima colonna):
- "stima", la risposta si basa su una stima visiva globale e fa menzione di una giustapposizione, senza altre precisazioni;
- “misura del perimetro”, effettuata con il righello, con dettagli dei calcoli o del perimetro ottenuto;
- “mista”, presa in considerazione simultanea di elementi caratteristici dell'area e del perimetro;
- "sovrapposizione", con ritaglio delle tre parti bianche e incollatura sulla parte grigia o con dettaglio del ricoprimento;
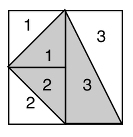
- "suddivisione", procedura prevista dall'analisi a priori (vedi figura nella sezione "Compito di risoluzione e conoscenza mobilitata"): la parte grigia è divisa in tre parti, ciascuna equivalente a uno dei triangoli bianchi;
- "pavimentazione o quadrettatura", le superfici sono quadrettate o ricoperte da pavimentazione che vengono contate.
{{img:8rmti_fr-6b|}}
__Stima__
In questa categoria di procedure troviamo risposte basate su una stima visiva globale o che evocano confronti per sspostamento di figure, ma senza alcuna traccia scritta. I tipi di spiegazioni sono piuttosto eterogenee. Si va dall'“autoconvinzione” (Es. 1) ad argomentazioni che fanno riferemento ai bordi del terreno (Es. 2) o all'addizione di triangoli (Es. 3). In questo tipo di risposta, il fatto che il prato sia in tre parti contro una sola per i fiori deve aver sicuramente influenzato i giudizi dei gruppi di allievi, di cui 17 su 24 hanno scelto la prima possibilità, 3 pensano che sia i fiori e 4 optano per l'equivalenza.
Esempio 1 //Noi pensiamo che la parte dell'erba sia la più grande e la parte del fiore la più piccola perché la parte del fiore è più piccola e la parte dell'erba è la più grande del giardino.//
Esempio 2 // Il campo fiorito sembra più grande ma quella più grande è il prato perché ha i bordi più grandi.//
Esempio 3 //Pensiamo che c'è più prato e meno giardino. Il triangolo piccolo e intero più un triangolo piccolo e intero formano un quadrato. Un quadrato più un triangolo grande a metà formano una forma di un quadrato più un triangolo grande a meta.//
(I tre triangoli "piccolo e intero" et "grande a meta" sono disegnati esplicitamente sul disegno dell'enunciato.)
__Misura del perimetro__
I gruppi che hanno scelto di misurare tutti i lati di diverse parti del giardino per confrontarli dovevano logicamente arrivare alla conclusione che il prato è il più grande. Ma sono solo 19 le risposte “prato” tra le 26 classi che hanno optato per questa procedura; ci sono anche 5 risposte “fiori” e 2 risposte “equivalenza”.
Esempio 4 //La maggior parte del giardino del signor Tordu è la parte grigia. Per trovare la risposta abbiamo calcolato col righello. E abbiamo addizionato i numeri. La risposta è 29 1/2.//
(Prima confusione tra les misure "4" dei due lati del quadrilatero e il perimetro "10" indicato nel triangolo di sinistre : 10 + 10 + 3 + 6 1/2 = 29 1/2. Seconda confusione per la parte bianca : 10 + 10 + 6 1/2 = 26 1/2 à la place de 10 + 10 + 15 1/2 = 35 1/2, peraltro annotato.
{{img:8rmti_fr-6c|}}
__Procedura mista__
Le risposte appartenenti a questa categoria di procedimenti sono poche, ma sembrano rivelare un cambiamento nelle rappresentazioni rispetto a quelle della categoria precedente basate sulle misurazioni laterali e sulla loro addizione sistematica.
Esempio 5 Una classe ha ritagliato i tre triangoli del prato per ricomporli in un unico poligono, un quadrilatero come la parte dei fiori, ma convesso. Ha poi calcolato i due perimetri, correttamente, trovando 17,9 e 21,5 cm. L'idea di conservazione dell'area nell'assemblaggio dei tre triangoli è chiaramente implicita, l'accento sul perimetro è messo solo al momento del confronto numerico. Non c'è più, come prima, una somma sistematica dei perimetri di tutte le parti. I lati comuni dei triangoli assemblati non vengono più presi in considerazione.
{{img:8rmti_fr-6d|}}
__Sovrapposizione__
La procédure per "sovrapposizione" è nettamente la più frequente, sia nella categoria 3 che nella categoria 4, scelto dal 40% delle classi di ogni livello. È anche la più efficace, dopo la procedura di “suddivisione”: sulle 44 classi che hanno sovrapposto le parti, 30 hanno concluso che erano equivalenti (68%). Il successo è maggiore nella categorie 4 (22 su 28, ovvero il 79%) che nella categorie 3 (8 su 16, ovvero il 50%).
Ci sono, tuttavia, alcune risposte errate sovrapposte che sembrano corrette:
Esempio 6 //La parte grigia è più grande di quella bianca, lo dimostriamo con questi pezzi. Ecco il risultato.//
l ricoprimento per collage sembra perfetto ma il commento lo smentisce, a causa dei filetti grigi che compaiono sotto i tre triangoli bianchi (vedi parte sinistra della figura seguente).
Esempio 7 //Abbiamo ritagliato il prato e abbiamo ricoperto i fiori e abbiamo conatatato che c'erano più fiori che prato.//
Il ricoprimento non è perfetto, gli allievi non osservano che ricoprimento non è perfetto e che a seguito del ribaltamento del grande triangolo rettangolo non c'è sovrapposizione del cateto minore sul lato del quadrilatero (vedi parte destra della figura seguente.) {{img:8rmti_fr-6e|}}
Un'osservazione generale si impone su questa categoria di procedure di “sovrapposizione”: nessuno dei gruppi ha accompagnato le proprie manipolazioni con argomentazioni. Che sia stata riconosciuta o meno l'equivalenza delle due parti, le spiegazioni fornite si basano solo su ritagli, sovrapposizioni o collage di oggetti reali: //forme bianche e grigie, parti di prato, pezzi, prato, fiori,// ecc. Le conclusioni sono espresse anche in termini di quantità fisiche o manipolazioni: //arriviamo alla stessa forma, le due parti sono la stessa cosa, ha la stessa dimensione, parti uguali, riusciamo a posizionarle, abbiamo visto che l'erba è più alto,..//. .
__Suddivisione__
La differenza tra le risposte di questa categoria e quella della precedente non è evidente ad una prima analisi perché anche gli allievi di questi gruppi ritagliano le diverse parti. È al momento della giustificazione che compaiono gli elementi caratteristici di queste spiegazioni: una partizione del quadrilatero in tre zone esplicitamente paragonate alle tre parti del prato. I disegni si avvicinano a quelli della categoria precedente dove compare il quadrato originale ma le tre parti non sono più semplici collage, sono piuttosto la trascrizione di un'immagine mentale dove il quadrato iniziale è non disegnato per comodità o per caso ma per mostrare la distribuzione in sei parti, equivalenti a due a due.
Molti altri esempi di queste procedure si possono trovare nell’articolo //Il conflitto area-perimetro / Le conflitti aire-perimetro// citato in bibliografia.
figure, comparaison, aires
==== Indicazioni didattiche ====
Questo problema è stato scelto come esempio per l'importanza dei problemi del Rally Matematico Transalpino nella pratica in classe, oggetto di un lavoro pratico a lungo termine presentato al convegno internazionale dell'ARMT a Faenza nel 2023. (Vedi bibliografia ).
Leggendo questo esempio, si comprende che l'attività deve svolgersi in un clima di ricerca libera e attiva, con manipolazioni (misure, tagli, collage, ecc.), confronti e scambi.
I dati dell'analisi precedente sono sufficienti per comprendere la ricchezza potenziale della ripetizione del problema in classe, per dare senso alla misurazione delle lunghezze e all'approccio al concetto di area. ==== Per andare più lontano ====
==== Bibliografia ====
Jaquet, F. (2000). Il conflitto area-perimetro / Le conflit aire-périmètre. In //L'educazione matematica// Anno XXI Serie VI-Vol.2 n.2 (Prima parte pp. 66-77). Anno XXI Serie VI. Vol.3 (Seconda parte pp. 126-143).
Marangoni, E. Sangiorgi, R. (2024). L'importanza del Rally Matematico Transalpino nella Didattica d’aula quotidiana / L’importance des problèmes du Rallye Mathématique Transalpin dans la pratique de classe. In //La Gazetta di Transalpino / La Gazette de Transalpie// 14. pp 17-24
==== Ripostiglio ====