l'eredità

Identificazione

Rally: 08.I.16 ; categorie: 7, 8 ; ambiti: GM, GP
Famiglie:

• CA - Confrontare aree
• CA/D - Confrontare aree con il ritaglio
• DEM - Fare una dimostrazione
• GDE - Organizzare una successione di relazioni in geometria deduttiva
• LA - Utilizzare misure di lunghezze e aree

Envoyer une remarque ou une suggestion

Sunto

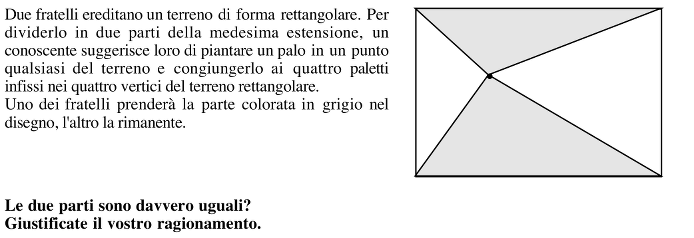
Osservare un rettangolo suddiviso in quattro triangoli da quattro segmenti che collegano un punto in comune all’interno del rettangolo a ciascuno dei quattro vertici. “Dimostrare” che la superficie totale dei due triangoli, la cui base è una lunghezza del rettangolo, è equivalente a quella totale degli altri due triangoli (aventi per base una dimensione del rettangolo).

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori

Capire che comunque si scelga il punto dove mettere il palo sul terreno rettangolare, se si conducono le parallele ai lati. la parte grigia e quella bianca sono entrambe composte dagli stessi quattro triangoli A, B, C, D. (aspetto connesso alla equiscomponibilità che prescinde dalla misura)

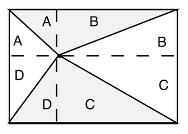
Oppure capire che comunque si scelga il punto dove mettere il palo sul terreno rettangolare, si individuano quattro triangoli aventi a due a due come base una delle due dimensioni del rettangolo e come somma delle altezze, l'altra dimensione, per cui anche se il punto dove si mette il palo cambia, la somma delle aree (di due triangoli aventi basi uguali) non cambia

Nozioni matematiche

area, rettangolo, triangolo, lunghezza, confronto di aree

Risultati

08.I.16

Su 60 classi della sezione SR

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta corretta con procedimento dimostrativo (del tipo indicato nell'analisi del compito)
• 3 punti: Risposta corretta e con spiegazione insufficiente (nessuna indicazione sulle rette che dividono il rettangolo, benché presenti nel disegno della risposta; nessuna indicazione sulla scomposizione delle parti bianche e grigie A, B, C, e D; nessuna giustificazione sull'uguaglianza dei triangolini, ...)
• 2 punti: Risposta corretta con ricorso a più di un esempio (il palo al centro o altro) con giustificazione sperimentale (misure e calcoli coerenti) oppure scomposizione (con ad esempio ritaglio) e ricomposizione delle parti bianche e grigie per formare due quadrilateri, senza giustificare la loro equivalenza ("si vede che ...")
• 1 punto: Risposta corretta con ricorso alla misura (sull'esempio dato) oppure risposta corretta senza alcuna spiegazione
  oppure risposta coerente con le misure effettuate su un solo esempio
• 0 punto: Spiegazione completamente errata o incomprensione del problema

Procedure, ostacoli ed errori rilevati

Come hanno risposto gli allievi alla richiesta di giustificazione, nel caso del problema “L’eredità”?

(Le parti sono veramente uguali. Abbiamo ritagliato il rettangolo della figura in vari triangoli che abbiamo disposti in modo da ottenere la stessa figura. Infine le abbiamo sovrapposte constatando che sono veramente uguali. Ciò è determinato dallo spostamento del centro.)

La giustificazione è, in questo caso, del tipo di quella riportata nell’analisi del compito. Se confrontiamo i due esempi, benché le due risposte siano entrambe corrette, il livello dei due ragionamenti è concettualmente diverso. Nel primo caso, come si vede, gli allievi hanno ritagliato il rettangolo in quattro parti, due bianche e due grigie, e ricomposto le parti dello stesso colore per ottenere due quadrilateri da confrontare. Non hanno però giustificato “formalmente” l’equivalenza delle due figure. Si sono “accontentati” di una sovrapposizione, per forza di cose approssimativa. Si tratta, in effetti di una argomentazione esplicativa di tipo locale, nel senso che “funziona” in questo caso, ma non si estende alla considerazione del fatto che comunque si scelga il punto dove mettere il palo sul terreno, l’equivalenza fra le due parti non cambia. Diversa situazione è quella che vediamo nel secondo esempio, dove gli allievi giustificano in maniera formale l’equivalenza. In una seconda parte dell’elaborato, però, gli allievi, passano alle misure e calcolano le aree delle due parti… per sentirsi più sicuri.

In effetti, gli allievi di 13/14 anni si trovano spesso in una fase di passaggio dall’evidenza di una prova empirica ottenuta con un calcolo su un esempio ad una giustificazione formale (Grugnetti, 2001).

Indicazioni didattiche

Dopo la risoluzione per gruppi e una discussione collettiva, gli allievi non solo devono essere convinti dell'uguaglianza delle due aree, grigia e bianca, ma devono rendersi conto che questa uguaglianza è indipendente dalla posizione della posta in gioco.

Devono constatare o "imparare" che né le stime, né le misurazioni effettuate con il righello, né le formule per l'area dei triangoli consentono loro di arrivare alla certezza a causa dell'impossibilità di ottenere misurazioni precise con il righello.

Devono anche notare che non esiste una scomposizione delle quattro parti in unità comuni poiché le dimensioni di questi triangoli dipendono dalla posizione del palo, ma che esistono numerosi modi per raggruppare i triangoli:

- Senza scomporli, è sufficiente spostare il triangolo bianco a sinistra, mediante una traslazione della lunghezza del rettangolo, verso destra, per formare, con il triangolo bianco a destra, un quadrilatero bianco le cui due diagonali sono perpendicolari e isometriche rispettivamente alla lunghezza e alla larghezza del rettangolo. Traslando verso il basso il triangolo nero superiore della larghezza del rettangolo, otteniamo anche un quadrilatero grigio con le stesse diagonali di quello bianco. Queste due traslazioni sono elementari per gli allievi abituati a manipolare. Basta ritagliare i quattro triangoli (e non semplicemente dirlo o farlo notare, purché l'insegnante sia convinto che, fino alle medie e alle superiori, alcuni alunni hanno bisogno di lavorare sugli oggetti del loro spazio e non solo sulle figure geometriche!)

- Scomponendo i quattro triangoli in otto triangoli rettangoli (come suggerito nella sezione "Compito di risoluzione e conoscenza mobilitata) riusciamo anche a convincerci dell'uguaglianza delle parti bianche e grigie.

Senza manipolazioni o spostamenti di figure, la valorizzazione didattica sarebbe assolutamente insufficiente per gli allievi che non hanno constatato l'ugualianza delle due parti del terreno né hanno saputo spiegarla. E, per beneficiare di questo lavoro manuale, gli allievi potranno convincersi che le uguaglianze sono verificate qualunque sia la posizione del palo.

L'insegnante può approfittare dell'attività per rivedere il concetto di traslazione (e isometria, che si applica sia alle lunghezze dei lati che alle aree). Può anche far notare agli allievi che esiste un modo molto semplice per trovare l'area di un quadrilatero le cui due diagonali sono perpendicolari: è la metà dell'area del rettangolo circoscritto.

Bibliografia

Grugnetti L. 2001. «Dimostrazione» e prove empiriche in problemi di geometria del RMT / «Démonstration» et preuves empiriques dans les problèmes de géométrie du RMT. In Atti del RMT / Actes du RMT. Vol. 2. pp 25 - 37