Drôle de panneau

Identification

Rallye: 13.I.14 ; catégories: 7, 8, 9 ; domaine: FN
Familles:

• MEQ - Etablir puis résoudre des (in)équations
• MEQ/EQ2 - Résoudre une équation du 2e degré
• RF - Traiter une relation fonctionnelle
• RF/TRI - Traiter une application quadratique

Remarque et suggestion

Résumé

Ce problème propose l’étude d’un triangle équilatéral dessiné sur un réseau triangulaire composé de triangles équilatéraux plus petits. Il propose de chercher s’il est possible de trouver un triangle dont l’aire de la bordure, composée d’un seul rang de triangles du réseau, est égale à l’aire du centre. Il conduit à l’étude d’un tableau de valeurs ou à celle des variations d’un trinôme du second degré dont les racines sont irrationnelles.

Enoncé

Tâche de résolution et savoirs mobilisés

- Comprendre ce qu’on entend par « bordure » et « triangle intérieur » en vérifiant les données : 16 et 33 petits triangles.

- Dessiner d’autres figures, constater, au passage, que sur le côté du triangle intérieur il y a toujours 3 petits triangles de moins que sur celui du grand triangle extérieur.

- Remarquer que le nombre de petits triangles équilatéraux qui forment ainsi un grand triangle (son aire en prenant un petit triangle pour unité) est égal au carré du nombre n de ces triangles disposés sur un de ses côtés (somme des nombres impairs de 1 à n).

- Rassembler ces valeurs pour différentes valeurs de n dans un tableau, par exemple :

- L’observation de la dernière ligne mène à la conclusion qui s’impose : il n’y a pas de valeur n qui permette d’obtenir un panneau ayant autant de triangles sur la bordure qu’à l’intérieur. C’est pour un triangle intérieur de côté 7 que I et B sont les plus proches (49 et 51). Au-delà, c’est I qui l’emporte (fonction « élever au carré ») sur B (fonction « multiplier par 6 et ajouter 9 »).

Ou : par un raisonnement algébrique, montrer que, si les aires I et B étaient égales, du fait que les aires des deux triangles exprimées en petits triangles sont des carrés, on obtiendrait l’équation (n+3)² – n² = n², d’où (n+3)/n = √2. On serait alors en présence d’une contradiction puisque √2 est irrationnel alors que n est un entier. Ce raisonnement permet d’affirmer qu’il n’y a pas de solution, même pour des bordures plus larges.

Ou : une étude de fonction du niveau 10 résout simplement le problème : elle consiste à étudier les variations de (n+3)² – 2n², et éventuellement étudier les racines de cette fonction trinôme qui s’écrit – n² + 6n + 9. La résolution algébrique donne la valeur positive non entière 3(1+√2), d’où la réponse négative à la question posée.

Dans le cadre fonctionnel, ce problème conduit à un exercice classique d’étude de trinôme. Mais cela ne peut se faire qu’au dernier niveau du RMT.

Notions mathématiques

fonction, triangle équilatéral, équation, trinôme du second degré, variations

Résultats

13.I.14

En 2005, ce problème de l’épreuve I du 13è RMT a été traité par 484 classes, réparties entre les catégories 7, 8 et 9. Les scores suivants ont été attribués :

Selon les critères de l’analyse a priori du problème :

• 4 points: Réponse correcte (impossible) avec une des justifications ci-dessus ou une autre, rigoureuse et détaillée
• 3 points: Réponse correcte avec tentative d’explication, par exemple à partir de plus de deux essais, sans erreur de calcul
  ou réponse avec justification complète mais avec une erreur de calcul
• 2 points: Réponse correcte, donnée à partir d’un ou deux essais seulement
• 1 point: Erreurs de calculs menant à l’affirmation qu’il y a une solution ou début de recherche (un ou deux panneaux dessinés) mais sans conclusion
  ou ou réponse correcte sans explication
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Ce problème est posé dans un cadre géométrique et son exploitation pour mettre en évidence les variations relatives des deux ensembles de triangles a été une difficulté non surmontée par beaucoup d’élèves qui n’ont pas fait le choix d’une inconnue.

Les 3/4 des classes n’ont pu donner le moindre début de résolution cohérente. Pour les catégories 7 et 8, ce problème s’avère trop difficile. Les outils nécessaires pour une résolution complète n’apparaissent qu’en catégorie 10.

Au niveau 9, on trouve des mises en équations correctes débouchant sur une équation trinôme. La résolution est alors tentée par tâtonnements ou essais numériques organisés. Le raisonnement arithmétique a été observé sur une copie de niveau 9.

Au niveau 10, l’étude des variations des nombres de triangles au centre et sur la bordure permet d’aller vers une conclusion.

Exploitations didactiques

Lors d’une activité en classe, pour amener les élèves à observer les variations des deux ensembles de triangles, on peut donner une planche de panneaux de différentes tailles dans lesquels les élèves sont appelés à dessiner les bordures et compter les petits triangles, comme pour ceux-ci :

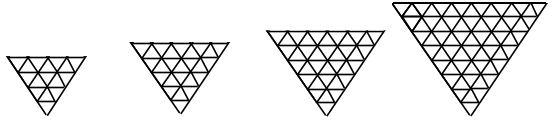
Ce qui donne de beaux dessins, mais ne conduit pas les élèves à changer spontanément de cadre pour une interprétation algébrique.

On peut aussi donner un tableau de valeurs à compléter tel que celui-ci, avec la question : « Le nombre de la dernière case peut-il être nul ? »

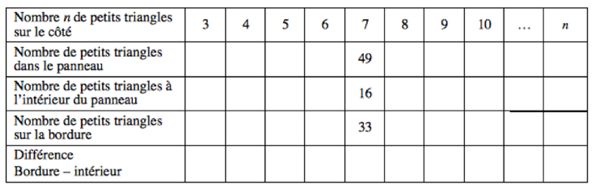
La plupart des élèves ayant reçu ce tableau le complètent correctement jusqu’à la dernière colonne qui leur donne l’équation résolvante :

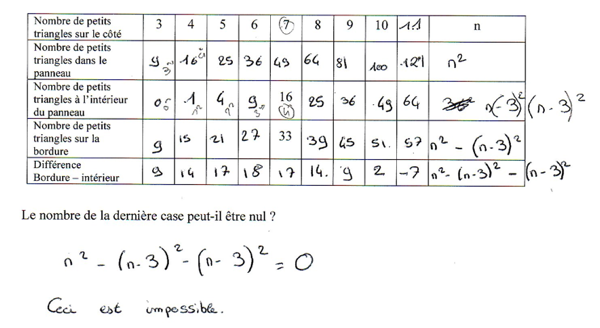
L’obstacle de la résolution algébrique de cette équation conduit ces élèves à une conclusion juste mais non justifiée. A ce niveau, les élèves pensent que seules les équations du premier degré peuvent être résolues formellement.

Bibliographie

Henry, M. Le concept de fonction dans les problèmes du RMT, Actes des journées d’études sur le Rallye mathématique transalpin, vol. 6, Parma 2006. Eds. Lucia Grugnetti, François Jaquet, Daniela Medici, M. Gabriella Rinaldi, ARMT, 2007, p. 151-168.

Krysinska, M. & Schneider, M. Émergence de modèles fonctionnels, les éditions de l’Université de Liège, col. Si les mathématiques m’étaient contées, 2010.

Groupe fonction (2010). Drôle de panneau. Etude ARMT (http://www.projet-ermitage.org/ARMT/doc/etude-fn4-fr.pdf)

(c) ARMT, 2005-2024