Piegature

Identificazione

Rally: 27.I.20 ; categoria: 10 ; ambiti: GP, GM
Famiglie:

• DEM - Fare una dimostrazione
• GDE - Organizzare una successione di relazioni in geometria deduttiva
• RD - Ricercare o utilizzare dimensioni
• TR - Costruire, utilizzare e/o effettuare una trasformazione geometrica

Remarque et suggestion

Sunto

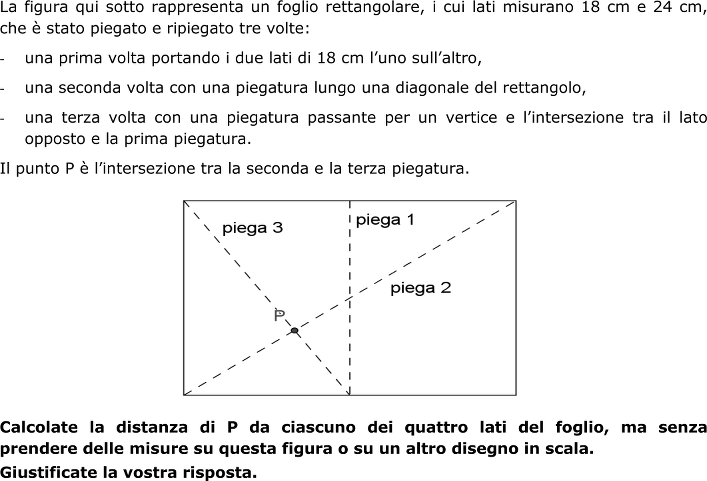
Determinare quanto dista dai quattro lati di un rettangolo il punto di intersezione fra una diagonale e il segmento che congiunge un vertice con il punto medio del lato opposto.

Enunciato

Compito per la risoluzione e saperi mobilizzati

Analisi a priori:

- Comprendere che per determinare la distanza di P dai lati del rettangolo è necessario tracciare le perpendicolari aio quattro lati passanti per P; si ottengono i segmenti PI, PH, PJ, PK per i quali bisogna calcolare la misura delle loro lunghezze.

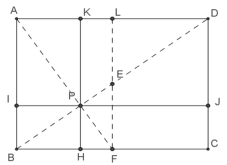
- Osservare che tre delle distanze da determinare sono le altezze dei triangoli con vertice P e che hanno come basi AD, AB, BF, che misurano rispettivamente 24, 18 e 12cm.

- Individuare i triangoli simili, ad esempio: APD è simile a BPF (avendo gli angoli congruenti) e il rapporto di similitudine è 2 in quanto AD=2BF. Dedurne che PK = 2PH= 2/3HK = 12CM, e PH=1/3HK = 6 cm.

- Analogamente, i triangoli APB e FPE (con E centro di simmetria del rettangolo) sono simili o omotetici e il rapporto di similitudine è 2 in quanto AB=2EF, poichè EF è metà di LF. Se ne deduce che PJ = 2PI e PI = 1/3IJ. Dunque PI = 8cm e PJ = 16 cm. Oppure:

- Arrivare alle conclusioni precedenti applicando il teorema di Talete, per esempio con le parallele AD e BC e le secanti AF, BD e HK.. Sapendo che BF è la metà di AD, si ha PA/PF = PD/PB = PK/PH = AD/BF =2; a partire da questo si determinano PK e PH. Procedere ugualmente con le parallele AB e LF e le secanti AF, BE e IJ per determinare PI e PJ. Oppure:

- Continuare ad operare mediante piegature utilizzando un foglio delle stesse misure o in scala al fine di trovare le relazioni fra i segmenti della figura. Per esempio, piegando il foglio lungo il segmento IJ si scopre che il punto M è il punto medio fra A ed I poiché piegando di nuovo, il punto B va a coincidere con A. Analogamente piegando lungo il segmento HK.

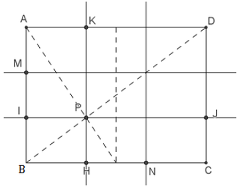
- Concludere che PH = 1/3 HK e PI = 1/3 IJ.

Nozioni matematiche

distanza, rettangolo, diagonale, vertice, mediana, omotetia, rapporto, Talete, mezzo, deduzione, dimostrazione

Risultati

27.I.20

Punti attribuiti su 2192 classi di 8 sezioni:

Secondo i criteri determinati nell’analisi a priori :

• 4 punti: Risposta corretta e completa (le distanze di P dai quattro lati del foglio sono: 6 e 12; 8 e 16, in centimetri) ben giustificata (riconoscimento di triangoli simili o l’applicazione del teorema di Talete)
• 3 punti: Risposta corretta, ma giustificazione parziale (per esempio, deduzione dei rapporti 1/3 e 2/3 con una spiegazione incompleta)
  oppure una coppia di distanza corrette (6 e 12) o (8 e 16) con una procedura ben giustificata e l’altra coppia di distanze sbagliata a causa di un errore di calcolo
  oppure tre distanze corrette e ben giustificate, e una dimenticata
  oppure soltanto due distanze di P dai lati non paralelli (una distanza per ogni coppia) ben giustificate
• 2 punti: Risposta corretta e completa ma con solo un abbozzo di spiegazione geometrica o una spiegazione percettiva (ad esempio ci sono dei triangoli uno doppio dell’altro)
  oppure solo le distanze di P da due lati paralleli del foglio ben giustificate geometricamente
• 1 punto: Risposta con una sola distanza calcolata correttamente e dimenticate o errate le altre
  oppure tentativi che mostrano che sono state riconosciute le distanze cercate ma che i calcoli non hanno portato a risposte corrette
• 0 punto: Incomprensione del problema
  oppure risposte corrette tratte da una costruzione su foglio quadrettato o misurate su un disegno in scala (contrariamente alla richiesta), sia che il disegno sia allegato o no.

(c) ARMT, 2019-2024