Les quatre piquets

Identification

Rallye: 21.II.18 ; catégories: 9, 10 ; domaines: GP, GM
Familles:

• ANG - Utiliser des angles et/ou mesures d'angles
• DEM - Effectuer une démonstration
• GEN - Générer et tester des solutions (partielles) possibles
• RD - Rechercher ou utiliser des dimensions
• RD/PY - Utiliser une relation classique

Remarque et suggestion

Résumé

Décider et justifier de l’alignement de trois points dans une situation où sont donnés un triangle équilatéral de côté 41 m et un point situé à 41 m et 71 m de deux de ses sommets, qui apparaît, par construction avec les instruments de dessin géométriques, comme le prolongement d’un de ses côtés.

Enoncé

Tâche de résolution et savoirs mobilisés

Comme pour de nombreux problèmes de géométrie déductive, una analyse a posteriori est absolument nécessaire pour comprendre les raisons de la très faible réussite.et ainsi améliorer l'analyse a priori rédigée avant la passation.

Une vingtaine de copies examinées montrent que la position des quatre points est approximativement déterminée et que l'alignement des trois points D, C et A est décidé visuellement, selon la précision du dessin.

La figure ABD est considérée proche d'un triangle rectangle et les élèves y appliquent le théorème de Pythagore dans le sens "direct": triangle rectangle + connaissance des côtés de l'angle droit (41) et (71) => possibilité de calculer la longueur de l'hypoténuse (√(41² + 71²) = √6722) et d'arriver ainsi à une valeur légèrement différente de 82 = 2 x 41; sans penser que, réciproquement, que si le théorème de Pythagore ne "marche pas" dans ce cas, c'est que la figure de départ n'est pas un triangle, mais un quadrilatère. L'obstacle est évident: faut-il faire confiance à sa vision dans le domaine de la géométrie ou aux calculs dans le domaine de l'arithmétique?

Il faut reconnaître. à leur décharge, que l'école ne se préoccupe pas, lors de l'étude du théorème de Pythagore, se sa réciprocité!!

Analyse a priori (a remplacer par une analyse a posteriori)

• La première tâche est de faire un dessin pour comprendre comment sont situés les piquets d’Antoine (A), de Bernard (B), de Clara (C) et de Danielle (D) : percevoir le triangle équilatéral ABC, choisir l’une des deux possibilités pour le point D qui correspond à la remarque de Danielle (dans l’alignement présumé de A et C).
• Remarquer qu’un croquis ne suffit pas pour conclure et chercher éventuellement à répondre à la question par une construction géométrique soignée à l’échelle, à la règle et au compas. Constater alors que les trois points A, C, D semblent alignés et qu’on ne peut pas rigoureusement conclure par une construction avec les instruments de dessin géométrique, au vu des limites de leur précision, comme le suggèrent les commentaires des quatre amis.
• Passer alors à une analyse de la figure formée par les quatre points et de ses propriétés pour la deuxième partie de la tâche : imaginer ou dessiner les segments, observer que le triangle ABC est équilatéral de côtés 41 m, le triangle BCD est isocèle de côtés 41 m, 41 m et 71 m.
• Envisager l’un ou l’autre des cas : A, C, D sont alignés (fig. I) ou A, C, D ne sont pas alignés (fig. II)

• Si l’on suppose que A, C, D sont alignés : AD est alors un segment de longueur 82. Le triangle ABD de côtés 41, 82 et 71 est rectangle, car les trois angles du triangle ABC valent 60 degrés, l’angle de sommet C du triangle isocèle BCD vaut 120 (180 – 60) degrés et les deux angles égaux chacun 30 degrés, l’angle ABD vaut 90 (60 + 30) degrés.
(Il y a encore d’autres manières de montrer que ce triangle est rectangle : inscrit dans un demi-cercle de rayon 41 ou décomposable en quatre triangles rectangles égaux…)

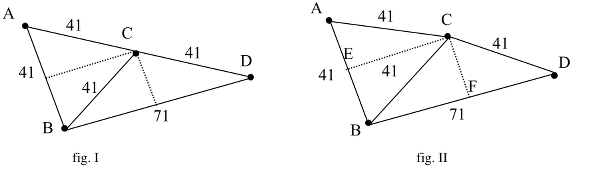
Mais dans cette hypothèse, le théorème de Pythagore n’est pas vérifié : 412 + 712 = 6722 ≠ 6724 = 822. On rejette l’hypothèse que A, C, D sont alignés. Remarquons que l’hypoténuse AD mesurerait 81,9878 m, à l’échelle 1/100 du dessin géométrique, la différence à repérer est de 1/10è de mm, invisible à l’oeil nu.

Ou bien, dans le second cas, on montre que A, C, D ne sont pas alignés (fig II): les deux triangles ACE et CDF ne sont pas égaux car leurs autres côtés sont respectivement différents:

Les deux triangles n’étant pas égaux, bien qu’ils soient rectangles et de même hypoténuse (41), leurs angles aigus sont respectivement différents, ainsi l’angle en C du triangle CDF est différent de l’angle en A de ACE (60°), donc l’angle en C du triangle isocèle BCD est différent de 120°, ajouté à l’angle en C de ABC (60°) cela donne un angle différent de 180° et par conséquent A, C, D ne sont pas alignés.

Notions mathématiques

géométrie, triangle rectangle, triangle isocèle, triangle équilatéral, somme des angles, Pythagore, côté, cercle inscrit, inégalité de triangles, racine carrée, approximations

Résultats

Points attribués sur 220 classes de 7 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte (non, ils ne sont pas alignés) avec une justification « théorique » géométriquement correcte (on ne pénalise pas les fautes d’écriture, d’unités, …)
• 3 points: Réponse correcte avec justification peu rigoureuse ou avec un chaînon manquant (par exemple dans le premier cas, on ne démontre pas que le triangle ABD considéré est rectangle, mais seulement qu’il ne vérifie pas Pythagore)
• 2 points: Réponse correcte avec explications à partir de propriétés de la figure, mais inadéquates ou insuffisantes (par exemple seulement la reconnaissance du triangle équilatéral et du triangle isocèle)
  ou réponse fondée sur une construction très précise avec les instruments de dessin géométrique, et cohérente (on accepte « oui » ou « non » pour autant que le dessin soit précis, que l’échelle soit indiquée) (avec les mesures de l’énoncé, un dessin ne permet pas d’être sûr de la réponse)
• 1 point: Réponse (correcte ou non) fondée seulement sur une construction géométrique approximative
• 0 point: Réponse (correcte ou non) sans explications
  ou incompréhension du problème

Bibliographie

Origine:  Rencontre dans le parc (19.II.16)

(c) ARMT, 2013-2024