
Banca di problemi del RMT
gp4-it
 |
Banca di problemi del RMTgp4-it |
|
Ricoprire una griglia 4x4 con il minor numero di pezzi scelti fra: due pentamini (L e Y), due tetramini (T), due trimini (L), e un domino.
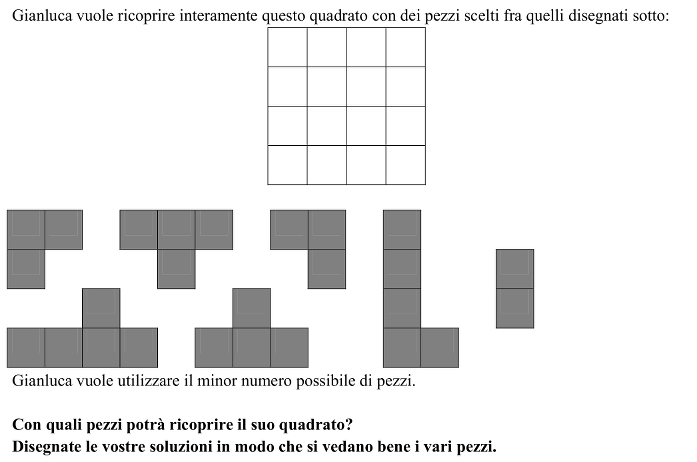
Trovare tutti i modi di ricoprire una griglia 4x4 con un minimo di pezzi scelti fra due pentamini (L et Y), due tetramini (T), due trimini(L) e un domino.
Determinare il numero dei quadretti della griglia (16) e di ciascuno dei sette pezzi (5, 5, 4, 4, 3, 3, 2), per trovare una scomposizione additiva di 16 che utilizzi il minor numero di termini fra quelli a disposizione (4) una che utilizza i due pezzi da 5 e i due pezzi da 3; l’altra che utilizza un pezzo da 5 (non la “L”), i due pezzi da 4 e uno da 3. Ad esempio:

Saper riconoscere i pezzi nelle loro diverse posizioni : permanenza o invarianza delle figure geometriche per traslazioni, rotazioni o simmetrie assiali (o ribaltamenti) e provare a disporre i pezzi corrispondenti alla scomposizione del 16. ( Si possono trovare le composizioni anche per tentativi successivi.)
Pavimentazione,aree, scomposizione additiva.
Punteggi su 458 elaborai di 6 sezioni italiane, svizzere e lussemborghese
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 3 | 9 (9%) | 7 (7%) | 13 (13%) | 65 (64%) | 7 (7%) | 101 | 2.53 |
| Cat 4 | 6 (6%) | 6 (6%) | 18 (18%) | 63 (63%) | 7 (7%) | 100 | 2.59 |
| Cat 5 | 2 (2%) | 5 (5%) | 15 (15%) | 66 (65%) | 13 (13%) | 101 | 2.82 |
| Totale | 17 (6%) | 18 (6%) | 46 (15%) | 194 (64%) | 27 (9%) | 302 | 2.65 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
La tabella dei punti attribuiti mostra che il problema è abbastanza facile.
L’età degli allievi non influisce particolarmente sulla riuscita.
Il solo errore, o difficoltà, incontrati sono legati alla ricerca di una seconda soluzione. Secondo la tabella, i due terzi dei gruppi hanno trovato una soluzione corretta (65%) e soltanto il 9 % le due soluzioni. E’ frequente che gli allievi più giovani si accontentino della prima soluzione trovata se non sono sollecitati da altre domande esplicite. Se si fosse aggiunto : « tutte » nella richiesta « Disegnate le vostre soluzioni in modo che si vedano bene i vari pezzi. » è probabile che più gruppi avrebbero proseguito nella loro ricerca.
Questo problema è utile per avviare all’acquisizione del concetto di misura d’area. Infatti la necessità di determinare il numero dei quadretti della griglia e di ciascuno dei pezzi e di trovare la scomposizione additiva di 16 che utilizzi il minor numero di termini fra quelli a disposizione, impone il passaggio dal registro geometrico a quello numerico.
Il problema “Quadrato da ricoprire” come La Sfida era già stato inserito dal gruppo di lavoro ad Arco in una serie di problemi ritenuti atti alla costruzione dell’idea di area e si ritiene che si presti ad essere usato nelle classi di cat.3,4,5 come problema di apprendimento soprattutto in relazione all’equiestensione per somma. Supportato dalla somministrazione avvenuta in alcune (9) classi di cat.7(ad inizio anno), i cui elaborati presentano le due soluzioni ottimali senza alcuna isometrica, il gruppo di lavoro ritiene che il problema possa essere utilizzato anche nelle cat.6,7, sia come verifica del possesso del concetto di equiestensione sia come problema di avvio per lo studio dell’equivalenza delle figure geometriche piane. Potrebbe essere interessante richiedere agli allievi anche la giustificazione del procedimento.
Esempi di elaborati di cat.7


Bisso C., Grugnetti L. (2006), « Approccio al concetto di area con problemi del RMT », Gruppo di lavoro n° 8, “ellealquadrato”, in R. Battisti, R. Charnay, L. Grugnetti, F. Jaquet (Eds.) RMT : des problèmes à la pratique de la classe / RMT : dai problemi alla didattica quotidiana, Actes des journées d’études sur le Rallye mathématique transalpin, Bourg-en-Bresse 2004, Arco di Trento 2005, ARMT, IUFM de Lyon-Centre de Bourg-en-Bresse, IPRASE Trentino , 267-276.
Bisso C., Grugnetti L. (2006), « Il ruolo dei problemi del RMT nella costruzione del concetto di area », in L. Grugnetti, F. Jaquet, D. Medici, M. G. Rinaldi, I problemi del RMT nella didattica quotidiana/ les problèmes du RMT dans la pratique de la classe, Parma 2006, ARMT, Dipartimento di Matematica dell’Università di Parma, Sezione ARMT di Parma, 25-36
Bisso C., Grugnetti L. (2006), « La costruzione del concetto di area con problemi del RMT », Gruppo di lavoro n° 6, “ellealquadrato”, in R. Battisti, R. Charnay, L. Grugnetti, F. Jaquet, D. Medici, M.-G. Rinaldi (Eds.) I problemi come supporto per l’apprendimento : il ruolo del RMT / Les problèmes au service de l’apprentissage : le rôle du RMT Parma 2006, ARMT, Dipartimento di Matematica dell’Università di Parma, Sezione ARMT di Parma, 169-187.
Douady R., Perrin-Glorian M.-J. (1989), « Un processus d’apprentissage du concept d’aire de surfaces planes », Educational studies in mathematics, 20, 387-424
ERMEL (2006), « Apprentissages géométriques et résolution de problèmes au cycle 3 », ed. Hatier, Paris Jaquet F. (2000), « Il conflitto aera-perimetro », L’educazione matematica, ed CRSEM, VI, 21, 2, (prima parte : n.2, 66-77, seconda parte : n.3, 126-143)
Rouche N. (1992), « Le sens de la mesure », Formation Didier Hatier
(c) ARMT, 2004-2024