Navi - bel affichage d'une fiche

Ornement grec

Identification

Rallye: 20.I.11 ; catégories: 5, 6, 7 ; domaine: GP
Familles:

Résumé

Une frise régulière est composée de bandes de même largeur en motif « grecque », de deux couleurs. Comparer les aires des parties de chacune des deux couleurs.

Enoncé

Tâche de résolution et savoirs mobilisés

- Faire le lien entre quantité de peinture et aire de chaque « zone », noire et jaune.

- Imaginer un quadrillage du motif d’après la largeur des bandes et se donner une unité d’aire (par exemple, celle d’un petit carré, u, dont le côté est la largeur des bandes).

- Déterminer, par comptage, l’aire de chaque zone (199 u pour la zone jaune et 197 u pour la zone noire).

Ou, repérer l’existence de motifs invariants par translation, répétés quatre fois et déterminer l’aire de chaque zone pour un motif de l’ornement, par comptage ou en procédant ligne par ligne, par exemple :

  pour la zone jaune :  8 + 8 + 1 + 6 + 3 + 5 + 3 + 6 + 1 + 8 = 49 (en unités u)
  et pour la zone noire : 8 + 7 + 2 + 5 + 3 + 5 + 2 + 7 + 8 = 47 (en unités u)

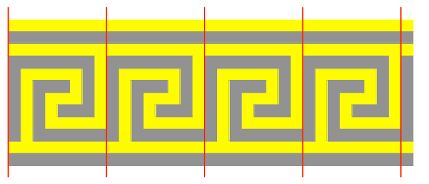
On obtient, pour les 4 motifs, 196 (en u) pour la zone jaune et 188 (en u) pour la zone sombre. Et en rajoutant la bande de droite on obtient 196 + 3 = 199 (en u) pour la zone claire complète et 188 + 9 = 197 (en u) pour la zone noire.

Ou pour chaque motif invariant par translation, découper les bandes claires sous forme de rectangle et les mettre bout à bout ; faire de même pour les bandes sombres ; évaluer la différence de longueur entre les deux bandes ainsi obtenues. La bande claire dépasse la bande sombre de 2 u, ce qui fait 8 u pour les quatre motifs. Compter sur la bande toute à droite de la frise que la bande sombre dépasse de 6 u la bande claire.

- Conclure qu’il faut plus de peinture jaune que de peinture noire.

Notions mathématiques

comparaison d’aires

Résultats

20.I.11

Points attribués sur 2417 classes de 24 sections:

Catégorie	0	1	2	3	4	Nb. de classes	Moyenne
Cat 5	336 (57%)	142 (24%)	52 (9%)	26 (4%)	29 (5%)	585	0.75
Cat 6	561 (56%)	262 (26%)	102 (10%)	44 (4%)	35 (3%)	1004	0.74
Cat 7	361 (44%)	235 (28%)	112 (14%)	38 (5%)	82 (10%)	828	1.09
Total	1258 (52%)	639 (26%)	266 (11%)	108 (4%)	146 (6%)	2417	0.86
Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème.

Selon les critères déterminés lors de l’analyse a priori :

4 points: Réponse correcte (Il faut plus de jaune que de noir) avec explications complètes, faisant clairement apparaître une différence de 2 unités entre les deux parties, ou avec les détails du comptage ou les « marques » de compensations, …
3 points: Réponse correcte avec aires exactes mais explications incomplètes
ou peu claires
2 points: Calcul ou dénombrement erronés mais démarche exacte,
ou réponse « plus de noir que de jaune » due à un comptage des quatre motifs seulement, sans remarquer que la colonne de droite n’appartient pas à l’un d’eux, avec le détail précis de l’écart entre 196 et 188.
1 point: Début de raisonnement (ou dénombrement) correct
0 point: Incompréhension du problème,

Procédures, obstacles et erreurs relevés

Ce tableau et les premières analyses de copies d’élèves de Suisse romande, Franche Comté, Cagliari) montrent à l’évidence que la tâche n’est pas à la portée des élèves de chacune des catégories concernée.

Lors de l’élaboration du problème, de l’analyse a priori, des lectures et des relectures, cette difficulté n’avait pas été soupçonnée, car on pensait que les élèves allaient quadriller le motif et compter des carreaux. (On est amené à se poser des questions sur les lecteurs et auteurs et on se demande s’il n’ont pas développé un « quadrillage du cerveau » à force d’inventer et d’analyser des problèmes sur réseaux quadrillés. )

Problème à soumettre au Groupe Géométrie plane.

Banque de problèmes du RMT