
Banque de problèmes du RMT
gp64-fr
 |
Banque de problèmes du RMTgp64-fr |
|
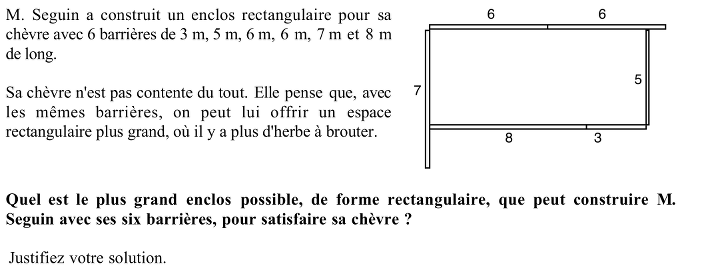
Construire le plus grand enclos possible, de forme rectangulaire, en utilisant six barrières de longueurs 3 m, 5 m, 6 m, 6 m, 7 m et 8 m.
- Calculer la longueur des barrières à disposition (35 m), en déduire le périmètre maximum possible (34 m),
- Procéder par essais successifs
ou travailler systématiquement à partir du demi-périmètre, 17 en essayant les dimensions 9 + 8 (solution la "plus proche du carré"), 10 + 7, 11 + 6,
- lorsque le rectangle 11 x 6 est trouvé, d'aire 66, vérifier que les autres disposition donnent des aires plus petites : 13 x 3, 11 x 5 (figure de départ), etc.
addition, multiplication, rectangle, aire, périmètre
Les résultats n'ont pas été conservés ou ne sont pas encore disponibles.
Ce travail de groupe s'est effectué durant le deuxième rencontre de Brigue, en collaboration entre des collègues d'Italie et de Suisse, sur la base des productions des groupes d'élève ayant participé aux finales de Parma, Siena et de Suisse romande, du 6e RMT (mai 1998). L’analyse de ces solutions a fait apparaître quatre aspects importants du problème :
1. Les procédures par essais
Cette stratégie, prévue par l'analyse a priori, ne doit pas être sous-évaluée dans la mesure où elle révèle une tendance naturelle de l'élève à procéder "par essais", lorsqu'il ne se sent pas obligé, par une demande précise, de mettre en oeuvre des processus de résolution spécifiques (par exemple : calcule le périmètre de ... , calcule l'aire de ... , résout l'équation suivante, ... ). Ce problème se prête particulièrement à cette procédure par essais : la longueur de l'enclos proposée par le dessin suggère déjà la solution.
2. La détermination d'un maximum
De nombreuses productions montrent les difficultés rencontrées par les élèves dans l'interprétation de l'expression "la plus grande possible" comme une recherche de maximum : "nous avons essayé d'échanger des barrières de la figure donnée, nous avons échangé la 6 et la 5 et l'aire est devenue plus grande que celle de la feuille" (classe de cinquième élémentaire, cat. 5); "M Seguin peut obtenir un enclos plus grand en disposant les barrières ainsi : ..." (classe de III Media, cat. 8). On peut ainsi supposer que, pour ces élèves, la question posée dans le problème est devenue : "trouvez un enclos plus grand que celui construit par M. Seguin".
D'autre part, on peut imaginer que les élèves ont lu plus attentivement la première partie de l'énoncé que la demande finale, même si celle-ci était en caractère gras : "Quel est le plus grand enclos possible, de forme rectangulaire, que peut construire M. Seguin avec ses six barrières, pour satisfaire sa chèvre ?"
3. Difficulté dans la justification de la solution
Une telle difficulté n'est pas liée au problème particulier de l'enclos, mais se rencontre souvent quand on demande à un élève de "justifier la solution". Dans la majorité des cas, il se contente de "raconter tout ce qu'il a fait" plutôt que d'expliquer la stratégie de résolution adoptée : "Nous avons additionné 8 et 3 = 11 m qui est un côté. ensuite 7 + 5 = 12m et les deux côtés qui mesurent 6m. Nous les avons utilisés comme base. Nous avons trouvé l'aire en faisant 11 fois 6 = 66m". (classe de III Media, cat 8).
4. Absence de vérification
Si l'enclos envisagé donne une aire plus grande que celui de M. Seguin ,les élèves, satisfaits, ne se préoccupent pas de vérifier si, en réalité, comme l'analyse a priori le prévoyait, d'autres dispositions des barrières donnent des aires plus petites ou, si il y a d'autres manières de placer les barrières qui conduisent au même résultat.
Proposition du groupe de travail
1. Afin d'éviter que le dessin avec une longueur d'enclos déjà optimale ne suggère la solution, obtenue alors par un simple échange d'une barrière de 6 m avec la barrière de 5 m, un nouvel énoncé a été élaboré, avec d'autres longueurs de barrières. Ces nouvelles longueurs permettent, en outre, de construire un plus grand nombre de rectangles au sein desquels il faudra chercher celui dont l'aire est maximale.
2. Puisque les classes finalistes sont peu nombreuses, il a été suggéré de proposer le nouveau problème de l'enclos dans une épreuve à laquelle participent toutes les classes.
3. Puisque l'analyse des résultats a montré que les élèves de catégorie 5 ont rencontré des difficultés majeures, il a été suggéré de présenter le nouveau problème en catégories 6 à 8.
4. Enfin le groupe a proposé de modifier le contexte du problème en remplaçant l'enclos de la chèvre par une terrasse de ciment à construire.
Le nouveau problème de l'enclos, du septième Rallye. Dans la première épreuve de la septième édition du RMT, la proposition du groupe de travail de Brigue s'est concrétisée par l'énoncé suivant : L'enclos de la chèvre (07.I.16)
(c) ARMT, 1998-2024