
Banque de problèmes du RMT
op61-fr
 |
Banque de problèmes du RMTop61-fr |
|
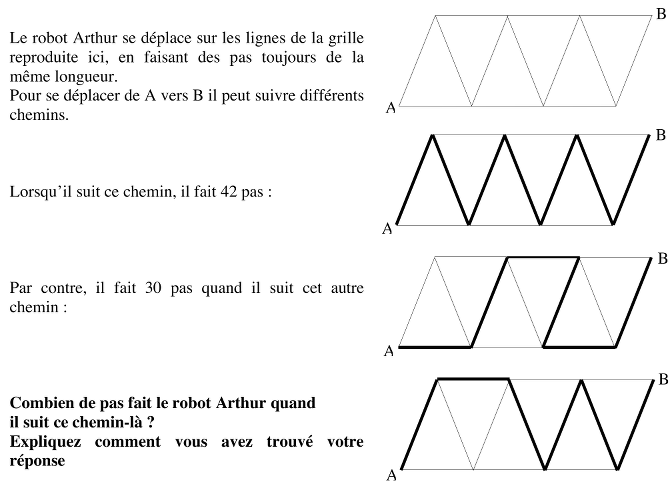
Sur un réseau composé de deux types de segments, horizontaux (h) et obliques (o), trouver la longueur d’un chemin composé de 1 h et 5 o connaissant la longueur d’un chemin de 7 o : 42 pas et celle d’un chemin 3 h et 3 o : 30 pas.
S’approprier le contexte et la situation :
Passer des objets physiques et mobiles aux figures géométriques qui représentent la « grille » composée de triangles et de segments sur lesquels peut se déplacer le robot.
- Il y a deux types de segments avec leurs caractéristiques : les segments horizontaux semblent tous égaux, les segments obliques (montants ou descendants) semblent aussi tous égaux, mais on ne sait pas si les deux mesures des longueurs de ces segments sont égales si on ne les compare pas avec une règle graduée ou un autre instrument de mesure.
- Comprendre que le pas est l’unité de mesure de longueur des segments, c’est-à-dire qu’on peut faire correspondre un nombre (de pas) à chacun des deux types de segments ; que ce nombre est entier car le mouvement des pas doit commencer à une extrémité d’un segment et se terminer exactement par la pose du pied du robot sur l’autre extrémité (le robot ne peut pas poser le pied vers la fin d’un segment et l’autre pied sur le segment suivant sans avoir passé par le sommet.
- Comprendre que les pas sont « toujours de la même longueur » pour chaque type de segment.
Passer du cadre géométrique au cadre numérique :
- Se rendre compte que pour trouver le nombre de pas du troisième chemin, il faut chercher préalablement le nombre de pas pour un segment oblique et le nombre de pas pour un segment horizontal.
- Déduire du premier chemin, parcouru en 42 pas et composé de 7 segments obliques tous égaux, que la longueur de chaque segment s’obtient par une addition répétée de 7 nombres égaux dont la somme est 42 ou par la multiplication par 7 d’un nombre inconnu conduisant au produit 42, ou par la division de 42 par 7. En conclure que chaque segment oblique est parcouru en 6 pas.
- Observer le second chemin, parcouru en 30 pas et formé de 3 segments obliques et de 3 segments horizontaux. Substituer 6 pas à chacun des trois segments obliques du second chemin, ce qui donne 18 pas (6 × 3) et en déduire qu’il faudra encore 12 (30 – 18) pas que pour parcourir les trois segments horizontaux et que, par conséquent chaque segment horizontal vaut 4 pas (12 : 3).
- Conclure que pour parcourir le troisième chemin, composé de 5 segments obliques et 1 segment horizontal, on peut leurs substituer les mesures calculées précédemment et calculer que le robot fera 6 × 5 + 1 × 4 = 34 pas.
opérations, nombres naturels, addition, soustraction, multiplication, division, unité de longueur, segment, pas, mesure, système d’équations, substitution
Points attribués, sur 760 copies de 17 sections:
| Catégorie | 0 | 1 | 2 | 3 | 4 | Nb. de classes | Moyenne |
|---|---|---|---|---|---|---|---|
| Cat 3 | 174 (52%) | 40 (12%) | 19 (6%) | 41 (12%) | 59 (18%) | 333 | 1.31 |
| Cat 4 | 153 (36%) | 84 (20%) | 18 (4%) | 72 (17%) | 100 (23%) | 427 | 1.72 |
| Total | 327 (43%) | 124 (16%) | 37 (5%) | 113 (15%) | 159 (21%) | 760 | 1.54 |
| Rappel: Le problème est résolu dans les conditions particulières du RMT: classe entière, élèves en autonomie complète, 5 à 7 problèmes à résoudre, une seule feuille de réponses par problème. | |||||||
L’analyse des copies a permis d’identifier trois erreurs fréquentes :
- Réponse 35 : les 7 segments du premier trajet sont considérés comme égaux, ce qui est correct et de longueur 6 (42 :7), les 6 segments du deuxième parcours sont aussi considérés comme égaux (ce qui est incorrect) et de longueur 5 (30 : 6). Le calcul de la longueur du troisième parcours est ainsi : 5 × 6 + 5 = 35 (pas).
Dans ce cas la confusion des segments se limite à ceux du deuxième trajet, la distinction est correcte sur le troisième trajet.
- Réponse 36 : tous les segments sont considérés comme isométriques. Les 6 segments du troisième parcours sont calculés selon la longueur déterminée sur le premier, ce qui conduit à la réponse 6 × 6 = 36 (pas). Il n’y a pas de vérification sur le deuxième parcours. Cette erreur semble renforcée du fait que la longueur du deuxième parcours, 30, est un multiple de 6.
- Réponse 30 : tous les segments sont considérés comme isométriques, mais cette fois-ci, c’est la longueur 5 qui est retenue, sans référence au premier parcours.
Les réponses correctes (près du tiers des copies) suivent la procédure décrite dans l’analyse de la tâche : calcul de la longueur d’un segment du premier parcours, (6 = 42 :7), substitution dans la deuxième relation 3 obliques et 3 horizontaux = 30, calcul de la différence pour arriver à la valeur des trois segments horizon taux (30 – 18 = 12).
La grande partie des échecs (près de la moitié) se situent au moment de l’appropriation lorsqu’il s’agit de passer du contexte à son interprétation géométrique et en particulier lorsqu’il s’agit de se rendre compte que les segments obliques de 6 pas sont déterminés par le premier parcours et ne peuvent pas varier pour le second. On relève à ce propos sur certaines copies des marques, parfois numérotées, qui doivent représenter ces pas.
L’unité de mesure, le pas, n’est pas toujours perçu comme une longueur de segment, mais comme une distance entre deux endroits où on été posés les pieds, successivement. Beaucoup de copies de catégorie 3 montrent que les élèves cherchent à mesurer les distances directement sur les figures, en cm.
Les élèves qui n’ont pas pu s’approprier le problème font des opérations avec les nombres donnés, du genre 42 + 30 = 72 ou 42 :2 = 21, 30 : 2 = 15, 15 + 21 = 36, ou encore additionnent les nombres de segments.
Les nombreuses incompréhensions du problème relevées en catégorie 3 montrent la nécessité d’une mise en commun après une première phase de recherche au cours de laquelle les élèves devraient pouvoir confronter leur perception de la situation, en particulier sur les pas qui déterminent des parties de segments qui deviennent l’unité de mesure qui ne varie pas.
Pour le passage aux opérations arithmétiques, il faut se rendre compte que les deux premiers parcours se traduisent par deux relations d’égalités entre les longueurs des segments (d’un point de vue algébrique on est en présence d’un « système d’équations » 7o = 42 et 3o + 3h = 30 conduisant à la solution o = 6 et h = 4 qui permettra d’arriver à 5o + 1h = 34 pour le troisième parcours).
La « résolution » de ces égalités fait appel aux opérations que les jeunes élèves rédigent sous des formes diverses.
Par exemple le premier parcours fait apparaître aussi souvent l’écriture 7 × 6 = 42 que 42 : 7 = 6, ce qui permet de rappeler leur équivalence.
Le deuxième parcours conduit à trois opérations qu’il s’agit d’ordonner : une multiplication par 3, 3 × 6 = 18, une soustraction 30 – 18 = 12 et une division (ou multiplication lacunaire 12 : 3 = 4.
On peut évidemment modifier les nombres et les parcours pour vérifier si les élèves ont donné du sens à ces opérations et sont capables de les reproduire avec de plus grands nombres.
Une variante du problème Les billes d’Arthur (24.II.5) a été conçue dans un contexte non géométrique. Les relations numériques sont les mêmes que dans le problème d’origine, mais les segments et parcours sont remplacés par deux types de boîtes de billes.
Une deuxième variante Le robot Robert, avec des nombres légèrement différents et des segments obliques nettement plus longs que les segments horizontaux permet de vérifier que la confusion de longueurs n'est pas seulement due à le perception visuelle ou à un obstacle plus élevé dans la conception de l’invariance d’une mesure de longueurs d’un parcours à l’autre.
(c) ARMT, 2012-2024