
Banca di problemi del RMT
sd188-it
 |
Banca di problemi del RMTsd188-it |
|
Calcolare il rapporto tra i volumi di due piramidi simili di base quadrata, sapendo che il lato della base della piramide grande misura 24 cm e che la base della piccola ha i lati paralleli a quelli della base della grande ed è inscritta in un terzo quadrato, i cui vertici sono i punti medi dei lati del grande quadrato.

- Rendersi conto che occorre determinare la misura dello spigolo di base e dell’altezza della piramide piccola o ragionare sul rapporto fra le misure delle due piramidi.
- Osservare che lo spigolo di base della terza piramide l3 è metà di quello della prima l1, cioè 12 cm.
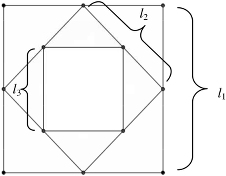
Oppure: calcolare successivamente lo spigolo di base della seconda piramide l2 e della terza piramide l3 mediante il teorema di Pitagora o osservando che l2 è metà diagonale del quadrato di lato l1, e l3 metà diagonale del quadrato di lato l2 : l2 = 12√2 et l3 = 12 (cm)
- Calcolare i volumi della prima e terza piramide V1 = 243/ 3 = 4608 e V3 =123/3=576(cm3).
- Calcolare il rapporto tra i due volumi 4608/576 = 8
oppure dedurre direttamente dal rapporto 2 tra le lunghezze corrispondenti della piramide grande e della piccola che il rapporto dei volumi è 23.
Su 305 classi di 9 sezioni partecipanti alla prova I del 23° RMT,
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 9 | 46 (29%) | 21 (13%) | 27 (17%) | 27 (17%) | 39 (24%) | 160 | 1.95 |
| Cat 10 | 35 (24%) | 28 (19%) | 15 (10%) | 26 (18%) | 41 (28%) | 145 | 2.07 |
| Totale | 81 (27%) | 49 (16%) | 42 (14%) | 53 (17%) | 80 (26%) | 305 | 2.01 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
(c) ARMT, 2015-2024