Le raisonnement évaluatif dans l’évaluation des compétences en mathématiques en fin de 4ème année primaire de l’enquête Mathéval
Anne-Marie Audemard, Marlène Rime
Introduction
L’enquête Mathéval vise à évaluer les nouveaux moyens d’enseignement des mathématiques utilisés dans les classes de Suisse romande. Elle comporte deux volets : le premier consiste en l’observation des réactions d’une approche socio-constructiviste des mathématiques au sein de la classe et de l’établissement, tandis que le deuxième a pour objectif de décrire les compétences et connaissances en mathématiques des élèves de 2ème et 4ème primaire qui suivent le nouveau programme d’enseignement (Antonietti, 2005). Dans le cadre de ce travail, nous nous chercherons à analyser le compte rendu de l’évaluation des compétences des élèves de 4ème primaire (Antonietti, 2005) sur la base du modèle théorique proposé par Arens (2006). Nous allons en effet essayer de voir si les conclusions auxquelles arrivent l’évaluation du programme sont valides en fonction du modèle présenté par Arens (2006).
Nous commencerons par présenter le modèle proposé par Arens (2006) et sur lequel nous allons nous baser pour la suite de notre travail. Ensuite, nous présenterons l’enquête Mathéval (Antonietti, 2005) en décrivant tout d’abord le programme, puis la question d’évaluation et enfin les méthodes, c’est-à-dire l’échantillonnage sélectionné et les instruments utilisés. Nous procèderons alors à l’analyse de cette enquête en nous intéressant au processus basé sur les évidences puis à celui basé sur les inférences que nous expose Arens (2006) avant de revenir sur les constats décrits par Arens (2006) afin de déterminer leurs validité dans l’enquête Mathéval. Enfin, nous discuterons nos résultats avant de conclure notre travail.
Le modèle proposé par Arens (2006)
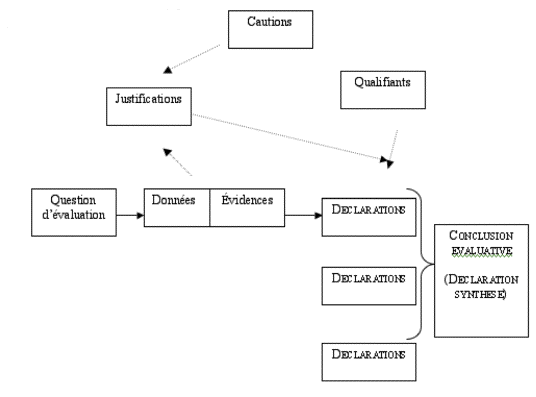
Arens (2006) définit l’évaluation de programme comme “une activité scientifique visant à établir la valeur ou le mérite d’un programme en s’appuyant sur des conclusions précises, justifiables, acceptables et légitimes” (House, 1993, in : Arens, 2006). Une évaluation de programme est ainsi considérée comme valide si l’argumentation conduisant au jugement de valeur est solide et relie les évidences aux déclarations. Deux processus permettent alors, selon elle, la construction de ce jugement : l’un est basé sur des évidences et le second sur des inférences.
Le processus basé sur les évidences traite les données pour en dégager des évidences en fonction de la question d’évaluation et permet de construire quelques conclusions évaluatives.
Le processus basé sur les inférences, quant à lui, nécessite de faire des inférences à partir des évidences en les soutenant par des arguments de types justifications, cautions ou qualifiants. Les justifications sont, selon Arens (2006), des “suppositions ou des prémisses qui relient logiquement une conclusion évaluative à l’évidence sur laquelle elle s’appuie”. Les cautions sont les lois, les règles, les principes, etc. sur lesquelles l’auteur d’une évaluation s’appuie pour appuyer son jugement. Finalement, le qualifiant détermine dans quels contextes (conditions) une justification est valide. L’argumentaire permet ensuite de construire un ensemble de déclarations par rapport à certains aspects du programme.
Les déclarations obtenues à l’aide des deux processus peuvent ensuite être résumées afin de construire une déclaration synthèse sur la globalité du programme, i.e. une conclusion évaluative.
L’enquête Mathéval
Description du programme
Dans le compte-rendu de l’enquête Mathéval (Antonietti, 2005), la description du programme est présentée ainsi :
« En 1997, de nouveaux moyens d’enseignement des mathématiques sont introduits dans les classes de Suisse romande. Ces nouveaux moyens n’apportent pas sur le plan des contenus mathématiques de grandes modifications. (…) L’innovation est d’ordre didactique. Les contenus didactiques sont les mêmes, en revanche la manière d’enseigner est fondamentalement différente. Selon cette nouvelle conception, très inspirée par la didactique des mathématiques française (Brousseau, 1998, in : Antonietti, 2005), l’enseignant a comme tâche de proposer à l’élève des situations dans lesquelles le savoir didactique puisse émerger. » (p.1).
Ainsi, l’approche proposée par le programme est présentée comme socio-constructiviste et prend appui sur la description faite par Brousseau (1998, in : Antonietti, 2005) des approches françaises.
Description de la question d’évaluation
La question d’évaluation est « de cerner les compétences et les connaissances en mathématiques mobilisables par les élèves de 2ème et 4ème primaire ayant bénéficié des nouveaux moyens » (Antonietti, 2005, p.2). Pour ce faire, les auteurs ont développé plusieurs questions auxiliaires:
- Comment les problèmes présentés aux élèves sont-ils construits ?
- De quelle manière les élèves résolvent-ils les problèmes auxquels ils sont confrontés ?
- Quel est le seuil minimal de compétences en mathématiques ?
- Les élèves parviennent-ils à atteindre ce seuil minimal de compétences ?
- Quels sont les progrès réalisés par les élèves ?
- Quels sont les qualités et les défauts des nouveaux moyens ?
Les questions auxiliaires sont introduites par la définition que les auteurs choisissent pour le terme de compétence, c’est-à-dire « un savoir-agir fondé sur la mobilisation et l’utilisation d’un ensemble de ressources » (Antonietti, 2005, p.2).
Description des méthodes
L’échantillonnage
Pour évaluer ces nouveaux moyens d’enseignement des mathématiques, les auteurs ont choisi un large échantillon. En effet, l’évaluation s’est faite dans sept cantons romands et dans vingt classes de chaque canton. Le nombre total de classes testées est alors au nombre de 140 ce qui correspond à un nombre total d’élèves interrogés de 2252.
Les instruments
Trois instruments ont été construits pour répondre aux questions de recherche : un questionnaire aux élèves, un questionnaire aux enseignants et les épreuves de mathématiques. Le questionnaire aux élèves comporte une partie générale qui permet de relever des informations sur l’âge, le sexe, la nationalité, la langue maternelle et le niveau socio-économique des élèves, ainsi que les retards scolaires éventuels. Une deuxième partie s’intéresse aux goûts des élèves pour les mathématiques et leurs préférences dans cette branche, ainsi qu’au plaisir qu’ils éprouvent à travailler seuls ou en groupe pendant les cours de cette matière.
Le questionnaire destiné aux enseignants se compose de quatre parties. La première permet d’obtenir des informations générales sur les enseignants (âge, sexe, expérience, effectif de leurs classes, taux d’occupation). La deuxième partie s’intéresse à l’utilisation qu’ils font des nouveaux moyens d’enseignement, tandis que la troisième porte son intérêt sur leur pratique et les manières qu’ils ont de gérer et d’organiser leur enseignement. Finalement, la quatrième partie porte sur leur façon d’évaluer les élèves et les difficultés qu’ils rencontrent pour le faire. L’épreuve de mathématique est construite de telle manière que chaque élève ne passe qu’une partie de l’épreuve complète sur la base d’un plan de testage connexe pour permettre les comparaisons entre les résultats des élèves. L’épreuve complète comporte en effet 8 blocs de problèmes qui contiennent chacun 7 problèmes. Ces blocs ont été répartis en cahiers à raison de 2 blocs par cahier. Chaque élève ne répond alors qu’à un seul cahier.
Chaque cahier est composé de deux parties distinctes. La première partie contiennent huit problèmes faciles et la seconde six problèmes plus difficiles, i.e. qu’ils « nécessitent une démarche tortueuse, souvent des tâtonnements, de l’intuition parfois » (Antonietti, 2005, p.26) pour parvenir à les réussir.
Les sources des problèmes sont de trois natures différentes. Seize problèmes viennent d’une enquête réalisée par l’IRDP en 1979 auprès d’élèves de cinquième année pour évaluer le programme de quatrième année, six problèmes proviennent de l’enquête Mathéval réalisée auprès des élèves de deuxième primaire en 2002 et 34 problèmes finalement ont été créés dans le cadre de cette enquête. Cette triple origine des problèmes permet de répondre aux questions d’évaluation. Les problèmes ont ensuite été répartis par un groupe d’experts dans les sept modules proposés par la méthode afin de s’assurer de la représentativité de l’épreuve, i.e. des problèmes pour apprendre à conduire un raisonnement, des problèmes pour approcher le nombre et lui donner du sens, des problèmes pour connaître l’addition, des problèmes pour connaître la multiplication, des problèmes pour explorer et organiser l’espace, des problèmes pour approcher les figures géométriques et les transformations du plan et des problèmes pour mesurer.
La difficulté des problèmes est déterminée lors de la passation de la même façon que les compétences acquises des élèves. De ce fait, les auteurs relèvent des différences de difficultés d’un cahier à l’autre. Les problèmes faciles sont ainsi considérés comme étant les mieux réussis et inversement.
Analyse
Le processus basé sur les évidences
Nous avons pu relever divers exemples qui s’appuient sur le processus basé sur les évidences. En effet, dans de nombreux cas, nous pouvons constater que les évidences entraînent des conclusions de manière directe. Voici une liste non exhaustive d’exemples :
Décomposer un nombre en unités, dizaines et centaines
Exemples d’items de Craies et Caramels :
| Combien de boîtes de dix caramels peut-on faire avec 4371 caramels ? |
Exemples d’items de Centaines, dizaines et unités :
| Combien y a-t-il de dizaines dans 4371 ? |
| Problèmes | Craies et Caramels, Centaines, dizaines et unités |
|---|---|
| Évidences | Le problème Craies et caramels est mieux réussi que Centaines, dizaines et unités |
| Déclarations | « L’aspect concret de l’énoncé de Craies et caramels permet donc aux élèves de mieux comprendre le sens des questions » (Antonietti, 2005, p.38) |
Comparer et écrire les nombres
- Le plus proche
Item 1 :
| Souligne parmi les nombres suivant celui qui est le plus proche de 1023 : 1203 1040 1230 2310 |
Item 2 :
| Et parmi les nombres suivants, souligne celui qui est le plus proche de 2001 : 1001 1002 3001 3002 |
| Problème | Le plus proche |
|---|---|
| Évidences | L’item 1 est mieux réussi que l’item 2 |
| Déclarations | 1. L’item dont le chiffre à approcher est le plus petit parmi les nombres proposés est mieux réussi que l’item dans lequel le chiffre à approcher se situe au milieu des chiffres proposés. 2. L’item dont les chiffres comporte de nombreux zéros intercalaires est moins bien réussi que l’item qui en comporte peu |
- Plus petit, plus grand
Exemple :
| Voici cinq chiffre : 4 1 9 0 3 a) Quel est le plus grand nombre qu’on peut écrire avec ces cinq chiffres ? b) Si on ne prend pas tous les chiffres, quel est le nombre le plus petit possible au-dessus de 1000 ? |
| Problèmes | Plus petit, plus grand |
|---|---|
| Évidences | Réussite plus élevée du deuxième item par rapport au second |
| Déclarations | « Le second item présente deux termes comparatifs qui s’opposent sémantiquement, puisque le nombre recherché doit être à la fois supérieur à 1000 et le plus petit possible. » (Antonietti, 2005, p.40) |
- Mille millions de mille sabords
Exemple :
| Écris en chiffres chaque nombre suivant : a) mille quarante b) dix mille quatre c) quatre cent quatre d) quarante mille quarante-quatre e) trois mille nonante-neuf f) neuf mille huit g) mille septante-trois |
| Problèmes | Mille millions de mille sabords |
|---|---|
| Évidences | 1. L’ensemble des items est réussi par 43% des élèves 2. Le taux de réussite pour tous les items comprenant des nombres de l’ordre de la centaine et du millier est élevé 3. Aucune erreur de confusion de chiffres n’est à signaler 4. Les erreurs les plus nombreuses portent sur l’omission d’un zéro 5. Le taux de réussite est plus élevé pour l’item (b) que pour l’item (d) |
| Déclarations | 1. « le transcodage de nombres supérieurs à dix mille s’avère plus délicat » 2. « les règles acquises pour les nombres inférieurs ne sont pas généralisées d’emblée » |
Résoudre des problèmes additifs
- La glace
Exemple :
| Jean a 1 franc et 70 centimes. Il s’achète une glace à 90 centimes. Combien lui reste-t-il ? |
| Problèmes | La glace |
|---|---|
| Évidences | 1. Le résultat correct est obtenu par 85% des élèves 2. Plus de 90% des réponses sont données en centimes 3. 76% des élèves posent l’opération bien que cela ne soit pas demandé explicitement |
| Déclarations | Si les élèves posent l’opération c’est vraisemblablement par effet de contrat didactique |
- Livraison de menhirs
Exemple :
| a) Au lever du soleil, Karwa livre des menhirs. A midi, il livre encore 102 menhirs. En tout il a livré 500 menhirs. Combien de menhirs a-t-il livrés au lever du soleil ? b) Warka travaille très vite. Cette semaine Warka ne fit que de la taille et sa réserve de menhirs a passé de 849 à 1021. Combien de menhirs Warka a-t-il taillés cette semaine ? |
| Problèmes | Livraison de menhirs |
|---|---|
| Évidences | 1. Les élèves réussissent mieux le premier item que le deuxième 2. Dans le premier item, plusieurs élèves ordonnent les nombres de manière à faciliter leurs calculs 3. La majorité des calculs sont écrits en colonnes 4. L’explicitation du calcul est faite par plus de 9 élèves sur 10 |
| Déclarations | « Le second item présente deux termes comparatifs qui s’opposent sémantiquement, puisque le nombre recherché doit être à la fois supérieur à 1000 et le plus petit possible.» (Antonietti, 2005, p.40) |
Le processus basé sur les inférences
La plupart des déclarations ne découlent pas directement des évidences. Pour celles-ci, les auteurs s’appuient sur des inférences de types cautions, justifications et qualifiants. Nous avons relevé certains exemples d’inférences qui permettent de passer des évidences aux déclarations:
- p.113-114 :
Evidence : « Au problème Le voyageur de commerce intergalactique, les résultats sont tout à fait inattendus puisque les élèves de 2P réussissent mieux que les élèves de 4P (taux d’échec plus bas et taux de réussite plus élevé). »
Inférences : « Si les deux items sont justes, alors le problème est réussi ; si un seul item est juste, alors le problème n’est réussi que partiellement et si aucun des items n’est juste, le problème est raté. »
Nous pouvons relever dans cet exemple d’inférence, les conditions de corrections. Nous pouvons donc supposer qu’il s’agit d’un qualifiant, puisqu’il donne les conditions dans lesquelles l’évidence est valable. En effet, les auteurs présentent par la suite, ce qu’il se produirait dans le cas où ces conditions seraient modifiées.
« Mais, si pour réussir le problème il suffisait de répondre correctement à l’item 2, alors l’ordre serait inversé : le taux de réussite serait légèrement élevé en 4P (56%) qu’en 2P (51%). »
Évidence : « Beaucoup d’élèves de 4P calculent correctement la durée du trajet entre Aldébaran et la planète du Dragon sans définir l’itinéraire ou dessiner la trajectoire. »
Inférence : « Or, le calcul correct de la longueur du trajet suppose une bonne représentation mentale du trajet. » Il s’agit dans ce cas d’une caution qui vient soutenir la déclaration suivante :
« l’absence de représentation graphique pourrait être interprétée comme un indice de progrès ». Une deuxième caution, faisant appel aux dires d’une tierce personne, vient renforcer cette déclaration : « On sait en effet que les élèves recourent de plus en plus aux stratégies numériques ou abstraites et de moins en moins aux stratégies concrètes ou graphiques, au fur et à mesure du développement des compétences en résolution de problèmes (Carpenter et Moser, 1982, in : Antonietti, 2005)
- p.115-116
Évidence : « En résumé, comparés à ceux de 2P, les élèves de 4P ont bien progresser en résolution de problèmes géométriques, alors qu’en résolution de problèmes numériques leurs compétences sont plutôt stables. »
Inférence : « Notons qu’en fin de 2P, les problèmes géométriques étaient moins bien réussis que les problèmes numériques, en raison notamment du peu d’importance qu’accordent certains enseignants aux modules géométriques durant les deux premières années. »
Nous rencontrons dans ce cas une justification qui présente une prémisse qui permet d’expliquer logiquement l’évidence afin de la relier à la déclaration suivante : « Les progrès significatifs des élèves de 4P en résolution de problèmes géométriques s’expliqueraient en partie par un regain d’importance accordée à la géométrie dès la troisième. » Dans la suite de ce paragraphe, nous pouvons rencontrer une nouvelle inférence : « Les conditions de passation différentes en 2P et en 4P l’apparente stabilité des compétences en résolution de problèmes numériques ». Cette inférence semble correspondre à un qualifiant, qui fournit les conditions dans lesquelles de tels résultats peuvent être obtenus. En effet, les auteurs poursuivent par une déclaration qui montre ce que pourraient être les résultats si les conditions étaient modifiées : « les taux de réussite totale ou partielle des élèves de 2P auraient sans doute été moins élevés en cas de passation individuelle et nous aurions peut-être enregistré des progrès significatifs des élèves de 4P. »
Évidence : « l’addition des taux d’échec et des taux de réussite partielle restent élevée même pour les problèmes géométriques. »
Les auteurs parviennent alors à la déclaration que « deux ans d’apprentissage n’ont pas suffi à la majorité des élèves pour atteindre le niveau des élèves plus doués ». Ils appuient cette déclaration par une caution, c’est-à-dire en reprenant les propos de Vergnaud et Durand (1976 , in : Antonietti, 2005) et Rogalski (1982, in : Antonietti, 2005) : « Le temps nécessaire au développement des compétences en résolution de problèmes est long, comme de nombreuses études l’ont montré ».
- p. 134-135
Évidence : « Les compétences en mathématiques varient légèrement avec l’âge : plus les élèves sont âgés, moins ils sont compétents. »
Sur la base de cette évidence, les auteurs parviennent à la déclaration suivante : « Pour mieux comprendre la situation, il est nécessaire de tenir compte du redoublement ». L’inférence qui relie l’évidence à la déclaration peut être défini comme une justification, car elle présente le lien logique entre les deux éléments : « Les élèves ayant redoublé sont en moyenne plus âgés que ceux qui n’ont subi aucun échec scolaire et leurs compétences en mathématiques sont en moyenne inférieures à celles de leurs camarades. Il s’en suit que globalement l’on observe une diminution des compétences avec l’âge ».
Retour sur les constats de Arens (2006)
Premier constat : « La démarche permettant d’arriver à des déclarations synthétiques ou à des conclusions évaluatives à partir des évidences n’est pas clairement saisissable à l’intérieur des rapports d’évaluation. Sa justification est douteuse, ce qui laisse place à l’interprétation du lecteur » (Arens, 2006, p.51).
En ce qui concerne l’enquête Mathéval, nous n’aboutissons pas au même constat. En effet, le raisonnement qui permet aux auteurs d’arriver à ces conclusions à partir des évidences est, en général, clairement explicité.
Deuxième constat : « Si les critères peuvent être aisément retracés, les standards, quant à eux, sont la plupart du temps absents ou ils prennent la forme de standards comparatifs qui s’expliquent par les choix comparatifs effectués » (Arens, 2006, p.52).
Un standard de compétence pour évaluer les nouveaux moyens d’enseignement des mathématiques a été fixé et a fait l’objet d’un chapitre. De plus, les auteurs semblent également s’appuyer sur des standards comparatifs pour évaluer le nouveau programme de mathématiques. En effet, les conclusions tournent aussi bien autour de comparaisons avec l’enquête Mathéval 2P de 2003, ainsi qu’avec l’enquête PISA de 2005 qui évaluaient les 9èmes et l’enquête réalisée par l’IRDP de 1979 (Hutin et al., 1991, in : Antonietti, 2005) qui évaluait l’ancien programme de mathématiques chez des élèves en début de 5ème que autour des standards établis par un groupe d’experts.
Troisième constat : « Les recommandations s’appuient d’avantage sur des justifications basées sur des autorités dans la matière que sur des évidences issues de déclarations. Les recommandations qui en résultent sont donc plus des faits qui suggèrent que les changements recommandés entraîneront automatiquement une amélioration sans être basé sur les résultats de l’évaluation. »
Concernant ce dernier constat, nous n’avons pu relever qu’une seule recommandation, dans cette enquête, ce qui rend difficile d’infirmer ou de confirmer le constat de Arens.
« Mais nous pensons que les élèves devraient se faire techniciens de l’addition, et de la multiplication ou du mesurage, ils devraient se faire, à un niveau de compétence défini, des professionnels de ces questions à l’encontre d’une certaine hiérarchie culturelle des actes intellectuels qui idolâtre l’amateur éclairé et tient en horreur le professionnel et le technicien » (Antonietti, 2005, p.159)
Cependant, nous pouvons remarquer que la construction de cette unique recommandation ne semble pas s’appuyer sur les évidences, mais bel et bien sur une justification basée sur une autorité, Chevallard (1991, in : Antonietti, 2005, p.159) : « Pour devenir « expert » en matière d’effectuation de sommes d’entiers relatifs, ou de résolution d’équations du second degré ou d’inéquations, ou de décomposition de fractions en éléments simples, en effet, il ne faut pas s’être contenté de savoir « résoudre le problème ». Il faut par exemple s’être demandé comment on pourrait encore résoudre telle équation que l’on sait déjà résoudre de telle ou telle manière. En d’autres termes, et pour le dire avec des mots empruntés à la sagesse populaire, il faut, cent fois, sur le métier, avoir remis son ouvrage. Il faut avoir longuement travaillé sa technique. »
Discussion
Dans l’enquête Mathéval, nous avons pu rencontrer dans le cadre du raisonnement évaluatif, tous les éléments décrits par Arens (2006). Nous avons en effet relevé à la fois des exemples de processus basé sur les évidences, ainsi que d’autres basé sur les inférences. Néanmoins, nous avons pu constater que le processus basé sur les évidences apparaissait surtout lors de la présentation des résultats de chaque problème. Par contre, dans les chapitres dans lesquels les auteurs tentent d’interpréter ces résultats, le processus basé sur les inférences prédomine. Cette constatation n’est pas relevée par Arens (2006), mais ce fait nous a paru intéressant. Il serait dès lors peut-être pertinent de vérifier si d’autres enquêtes évaluatives fonctionnent selon ce schéma.
Dans les deux processus, nous avons pu mettre en évidence que tous les éléments inhérents à ceux-ci étaient utilisés par les auteurs. Nous avons en effet rencontré des évidences et des déclarations, ainsi que des justifications, des cautions et des qualifiants. Ceci nous permet alors de supposer que le modèle décrit par Arens (2006) correspond et s’applique à ce qui se passe réellement dans les enquêtes évaluatives.
Concernant les constats que Arens (2006) présente en dernière partie de son article, nous avons pu constater qu’un seul d’entre eux semblent pouvoir s’appliquer à cette enquête. En effet, l’unique recommandation relevée nous permet de supposer que le troisième constat de Arens (2006) semble se confirmer dans cette enquête, puisqu’elle est construite sur la base d’une justification qui prend appui sur une autorité. Par contre, nos recherches nous ont permis de relever tous les éléments du modèle et ceux-ci sont exprimés de façon explicite, ce qui permet de valider les déclarations ou conclusions évaluatives des auteurs. Ceci va dès lors à l’encontre du premier constat d’Arens (2006). De plus, nous avons montré que certains standards ont bien été déterminés par les auteurs, contrairement à ce qu’Arens a rencontré dans son étude (2006). De même, les auteurs s’appuient sur des standards comparatifs pour construire leurs conclusions évaluatives. Ceci va d’une certaine manière à l’encontre de ce que décrit Arens (2006) dans son deuxième constat. Nous avons pu remarquer que les auteurs avaient, tout au long de leur enquête, répondu à leurs questions auxiliaires.
Conclusion
Au terme de ce travail, nous sommes en mesure de prétendre que le modèle décrit par Arens (2006) peut être applicable dans la réalité d’une enquête évaluative et que celui-ci permet de suivre le raisonnement évaluatif construit par les auteurs d’une manière claire. Néanmoins, nous sommes arrivées à la conclusion que ses constats ne pouvaient s’appliquer entièrement à cette étude.
Bibliographie
Antonietti, J.-P. (Ed) (2005). Évaluation des compétences en mathématiques en fin de 4e année primaire : Résultats de la seconde phase de l’enquête Mathéval. Neuchâtel: IRDP.
Arens, S. A. (2006). L’étude du raisonnement dans les pratiques évaluatives. Mesure et évaluation en éducation, 29(3), 45-56.