
Banca di problemi del RMT
fn4-it
 |
Banca di problemi del RMTfn4-it |
|
Questo problema propone lo studio di un triangolo equilatero composto da triangoli equilateri più piccoli. Si chiede se e’ possibile costruire un triangolo che abbia la superficie del bordo uguale alla superficie dei triangolini che compongono il centro Ciò porta alla costruzione e allo studio di una tabella di valori o a quella della scomposizione di un trinomio di secondo grado con numeri irrazionali.

- Comprendere quello che si intende per «bordo» e «triangolo interno» verificando i dati: 16 e 33 triangolini.
- Disegnare altre figure e constatare, per tutte, che sul lato del triangolo interno ci sono sempre 3 triangolini di meno che su quello del triangolo grande esterno.
- Notare che il numero dei triangolini equilateri che formano un triangolo grande (prendendo un triangolino come unità per calcolare la sua area) è uguale al quadrato del numero n dei triangoli disposti su uno dei suoi lati (somma dei numeri dispari da 1 a n).
- Raccogliere questi dati per differenti valori di n in una tabella, per esempio:

- L’osservazione dell'ultima riga (B-I) porta alla conclusione che si impone: non esiste un valore di n che permette d’ottenere un cartello con un numero di triangoli sul bordo pari a quello dell'interno. E' possibile per un triangolo interno di lato 7 che I e B sono il più vicino possibile (49 e 51). Per i numeri successivi, è I che supera (funzione «elevare al quadrato») B (funzione «moltiplicare per 6 e aggiungere 9»).
Oppure: con un ragionamento algebrico, mostrare che, se le aree I e B fossero uguali, per il fatto che le aree dei due triangoli espresse in unità triangolini corrispondono a quadrati, si otterrebbe l’equazione (n+3)2 – n2 = n2, da cui (n+3)/n = √2. Si evidenzierà la contraddizione poiché √2 è irrazionale mentre n è un intero. Questo ragionamento permette d’affermare che non ci sono soluzioni, anche per bordi più ampi.
Oppure: con uno studio di funzione per il livello 10 il problema è risolvibile facilmente: ciò consiste nello studiare le variazioni di (n+3)2 – 2n2, ed eventualmente studiare le radici di questa funzione trinomia che si scrive – n2 + 6n + 9. La soluzione algebrica dà il valore positivo non intero 3(1+√2), da cui la risposta negativa alla domanda posta.
Nell'ambito funzionale, questo problema conduce ad un esercizio classico di studio di un quadrato di un trinomio. Ma questo è possibile solo per il livello più elevato del RMT.
funzione, triangolo equilatero, equazione, trinomio di secondo grado, variazioni
Nel 2005, questo problema della prova I del 13° RMT è stato svolto da 484 classi, suddivise fra le categorie 7, 8 e 9. Sono stati attribuiti i seguenti punteggi:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 7 | 192 (78%) | 40 (16%) | 6 (2%) | 5 (2%) | 4 (2%) | 247 | 0.34 |
| Cat 8 | 119 (64%) | 29 (16%) | 19 (10%) | 10 (5%) | 8 (4%) | 185 | 0.7 |
| Cat 9 | 48 (92%) | 4 (8%) | 0 (0%) | 0 (0%) | 0 (0%) | 52 | 0.08 |
| Totale | 359 (74%) | 73 (15%) | 25 (5%) | 15 (3%) | 12 (2%) | 484 | 0.45 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Questo problema è posto in un registro geometrico e la sua utilizzazione mette in evidenza che le variazioni relative dei due insiemi di triangoli è stata una difficoltà non superata per molti degli allievi che non sono ricorsi all’uso di un'incognita.
Per i 3/4 delle classi non è stato possibile dare neppure un inizio di soluzione coerente, per i motivi che saranno analizzati di seguito. Per le categorie 7 e 8, questo problema è risultato troppo difficile. Gli strumenti necessari per una risoluzione completa non compaiono che in categoria 10.
A livello 9, si trovano delle messe in equazione corrette che portano ad un'equazione trinomia. La risoluzione è, allora, data per tentativi o con ricerche numeriche organizzate. Il ragionamento aritmetico è stato osservato in un elaborato del livello 9. A livello 10, le variazioni del numero dei triangolini al centro e sul bordo permettono di giungere ad una conclusione.
Durante un'attività in classe, per condurre gli allievi ad osservare le variazioni dei due insiemi di triangoli, si può dare una serie di cartelli di differenti misure sui quali gli allievi possono disegnare i bordi e contare i triangolini, come in questo esempio:
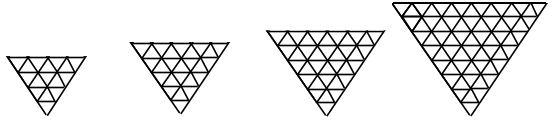
Si ottengono cosi’ disegni di buona qualità ma questa attività non porta gli allievi a passare spontaneamente al registro algebrico.
Si può anche dare una tabella di valori da completare come quella seguente, ponendo la domanda: "Il numero dell'ultima casella può essere zero?"
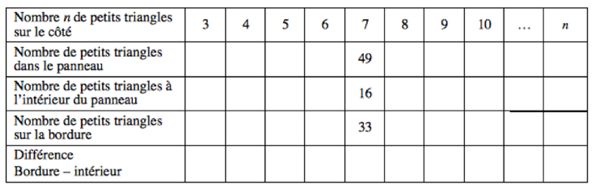
La maggior parte degli allievi che hanno ricevuto la tabella la completano correttamente fino all'ultima colonna che permette loro di individuare l'equazione risolutiva:
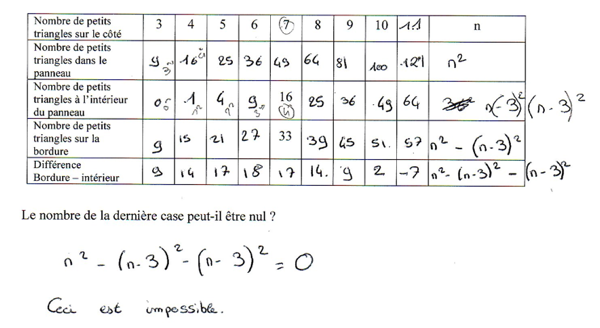
L'ostacolo alla soluzione algebrica di questa equazione porta gli allievi a questa soluzione corretta ma non giustificata. Gli allievi a questo livello ritengono che solo le equazioni di primo grado possano essere risolte formalmente.
Henry, M. Le concept de fonction dans les problèmes du RMT, Actes des journées d’études sur le Rallye mathématique transalpin, vol. 6, Parma 2006. Eds. Lucia Grugnetti, François Jaquet, Daniela Medici, M. Gabriella Rinaldi, ARMT, 2007, p. 151-168.
Krysinska, M. & Schneider, M. Émergence de modèles fonctionnels, les éditions de l’Université de Liège, col. Si les mathématiques m’étaient contées, 2010.
Groupe fonction (2010). Che cartello strano. Studio ARMT (http://www.projet-ermitage.org/ARMT/doc/studio-fn4-it.pdf)
(c) ARMT, 2005-2024