
Banca di problemi del RMT
fn6-it
 |
Banca di problemi del RMTfn6-it |
|
Trovare le dimensioni di un rettangolo di area 40 m2 e perimetro parziale (tre lati) 20 m, che nel contesto é un recinto circondato da una rete (equazione di secondo grado con radici irrazionali che possono essere approssimate).
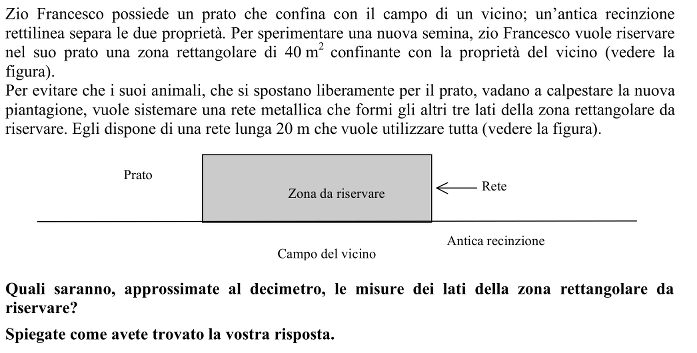
Si tratta anzitutto di appropriarsi della situazione e di riconoscere che i lati del recinto possono variare mentre restano costanti l’area del rettangolo e la lunghezza della recinzione.
Quindi occorre tradurre in equazioni le relazioni tra le variabili. Ad esempio, se si indica con x la lunghezza del lato del rettangolo parallelo alla vecchia recinzione (base) e con y quello perpendicolare (altezza), si ottengono le equazioni: xy = 40 e x + 2y = 20.
A questo punto, si aprono diversi percorsi.
1) Operare per tentativi, eventualmente aiutandosi con una tabella. I tentativi possono essere effettuati fissando il valore di una variabile, ricavando quello dell’altra variabile da una delle due equazioni e utilizzando la seconda relazione per controllo. Oppure, in alternativa, si possono far variare contemporaneamente i valori di x e y nelle due formule.
2) Riconoscere l’insieme delle due equazioni come un sistema, nel senso che le soluzioni da trovare per x e y devono essere valide per entrambe le equazioni scritte. Per risolverlo, sostituire una variabile con una funzione dell’altra per ottenere un’equazione in una incognita; per esempio sostituire nella seconda equazione y con 40/x, ed ottenere l’equazione di secondo grado: x2 – 20x + 80 = 0.
La risoluzione di questa equazione può avvenire mediante la formula risolutiva (solo per la cat.10) o per approssimazioni successive. In questo caso è possibile considerare la funzione y = x2 – 20x + 80 ed assegnare valori alla variabile x in modo da trovare due valori di y di segno opposto. La ricerca può essere fatta in un primo tempo con valori interi di x e poi raffinata con la suddivisione in decimi degli intervalli trovati.
3) A partire dalle due relazioni xy = 40 e x + 2y = 20, tracciare i grafici delle curve corrispondenti, individuarne i due punti di intersezione e interpretare le loro coordinate nel contesto del problema. Un'altra possibile risoluzione grafica consiste nel tracciare il grafico della parabola y = x2 - 20x + 80 ed individuarne le intersezioni con l'asse delle ascisse. Una volta trovate le due soluzioni del problema, occorre presentarle con l'approssimazione richiesta.
variabile, funzione, equazione, grafico cartesiano, approssimazione, numeri reali
Il problema è stato assegnato a 142 classi della categoria 9 e 108 della categoria 10
Si riportano i risultati nella seguente tabella:
| Categoria | 0 | 1 | 2 | 3 | 4 | Nb.classi | Media |
|---|---|---|---|---|---|---|---|
| Cat 9 | 74 (74%) | 13 (13%) | 10 (10%) | 2 (2%) | 1 (1%) | 100 | 0.43 |
| Cat 10 | 60 (61%) | 13 (13%) | 8 (8%) | 7 (7%) | 11 (11%) | 99 | 0.95 |
| Totale | 134 (67%) | 26 (13%) | 18 (9%) | 9 (5%) | 12 (6%) | 199 | 0.69 |
| Si ricorda che il problema è stato affrontato nelle condizioni particolari del RMT: intera classe, allievi in completa autonomia, da 5 a 7 problemi da risolvere, un solo foglio risposta per problema. | |||||||
Secondo i criteri dell’analisi a priori:
* oppure un risultato ottenuto per tentativi non organizzati
Preliminarmente si segnala la presenza di un ostacolo nell’interpretazione della figura. Da essa vengono erroneamente dedotte informazioni supplementari, ad esempio che la base debba essere maggiore dell’altezza (con conseguente unica soluzione del problema) oppure che vi sia un rapporto fra i lati che si debba riconoscere attraverso una misura diretta. È possibile che l’enfasi attribuita alla figura dal testo del problema (“vedere la figura” ripetuto due volte) sia correlata a questa interpretazione. Un’altra possibile ambiguità del testo è rappresentata dalla richiesta “Spiegate come avete trovato la vostra risposta” che può far pensare ad una soluzione unica.
Le procedure più utilizzate sono la ricerca per tentativi (cat.9) e la risoluzione dell’equazione di secondo grado (cat.10) mediante una formula risolutiva.
Nel primo caso (procedura per tentativi) si nota la difficoltà di organizzare tentativi con numeri decimali e di descrivere i tentativi fatti, che spesso restano impliciti. Inoltre la ricerca viene arrestata al primo tentativo favorevole, perdendo così una delle due soluzioni del problema. Nel secondo caso (equazione) si evidenziano difficoltà di natura algebrica, legate alla risoluzione dell’equazione di secondo grado. In entrambi i casi, ma soprattutto nella risoluzione algebrica in cui le soluzioni dell’equazione vengono scritte in forma simbolica mediante radicali, emerge il problema di che cosa significhi l’approssimazione al decimetro richiesta.
Come già detto, tra le procedure errate si segnala la deduzione dalla figura di un rapporto fra i lati (esempio 1:3 oppure 1:4), dato che viene utilizzato al posto di uno di quelli del problema.
In diversi elaborati si osserva l’ipotesi implicita (dedotta dalla figura) che la base debba essere maggiore dell’altezza, limitazione che porta a non considerare o ad escludere una delle due soluzioni del problema.
Nel contesto della gara, il problema ha ottenuto una bassissima percentuale di successi (soprattutto in cat.9). In effetti questo problema, oltre alla capacità di matematizzare la situazione attraverso la scrittura di un sistema e a quella di determinare le soluzioni dell’equazione risolvente in modo algebrico o grafico, richiede altre capacità, come quella di comprendere la situazione senza farsi condizionare dalla figura proposta e quella di riconoscere come numeri irrazionali le due coppie di soluzioni ed eventualmente di approssimarle.
La ricchezza del problema tuttavia costituisce una risorsa per l’insegnante che lo può utilizzare in diversi momenti del percorso scolastico e con diverse finalità. In funzione di tali obiettivi, l’insegnante può anche integrare o parzialmente modificare le richieste del problema, tra le quali quelle per risolvere le segnalate ambiguità del testo originale.
Si propongono alcuni esempi:
- Scelta delle variabili e confronto fra le equazioni ottenute. Il problema può inserirsi in un percorso di avvio alla risoluzione di problemi algebrici. Esso costituisce un esempio di situazione in cui la scrittura dell’equazione risolvente passa attraverso l’impostazione di un sistema e dipende dalla scelta delle variabili (si ottengono equazioni simili ma diverse se x e y indicano rispettivamente la base e l’altezza del rettangolo o vice versa).
- Introduzione delle equazioni di secondo grado: il problema può essere utilizzato per far nascere l’esigenza di un metodo rapido ed efficace per la risoluzione di tali equazioni contrapposto ad una lunga e non sempre affidabile ricerca per tentativi. A questo scopo il problema può essere lasciato sostanzialmente nella sua forma originale.
- Rappresentazione di funzioni: il problema può essere utilizzato per dare esempi di funzioni nate da una situazione geometrica e per sottolineare il rapporto di dipendenza fra le variabili. A tal fine potrebbe essere aggiunta la richiesta esplicita di una rappresentazione (in forma di tabella o di grafico) della funzione. In mancanza di tale richiesta si è osservato, infatti, che il ricorso allo strumento funzione (in particolare nel suo registro grafico) non è spontaneo. Al problema si possono associare vari tipi di grafici (iperbole e retta o parabola, con piccole variazioni anche in relazione alla scelta delle variabili). Uno strumento come Geogebra può essere utilizzato per sollevare lo studente dagli aspetti tecnici della costruzione del grafico e focalizzare l’attenzione sull’interpretazione del grafico stesso. Un confronto fra i grafici delle figure 1 e 2 porta ad una riflessione sulle soluzioni del problema.

Il grafico della figura 1 fornisce i due valori delle incognite x e y, mentre quello della figura 2 fornisce solo i valori di x, mentre quelli di y devono essere ricavati dalla relazione utilizzata per la sostituzione.
- Approssimazione: il problema può essere utilizzato per una riflessione sulla natura dei numeri che lo risolvono. Si tratta infatti di numeri irrazionali, che possono essere scritti in forma simbolica mediante radici quadrate ma che nella situazione reale (in cui sia previsto ad esempio l’acquisto della recinzione) è necessario approssimare. Una possibile variabile didattica del problema può essere il grado di approssimazione richiesta. Si sottolinea che, rappresentando le funzioni con un software come Geogebra, la comprensione del concetto di numero irrazionale può essere favorita grazie all’esplorazione del grafico mediante lo strumento “zoom”: il numero irrazionale, che inizialmente sembra “a portata di mano”, nei successivi ingrandimenti diventa sempre più “sfuggente” mentre aumentano le cifre decimali dei numeri che lo racchiudono. Nella figura 3 è rappresentata una delle soluzioni del problema.

Henry, M. & Rizza, A. Six questions sur la notion de fonction dans les problèmes du RMT, Actes des journées d’études sur le Rallye mathématique transalpin, vol. 8, Brigue 2008. Eds. Lucia Grugnetti & François Jaquet, ARMT, 2009, p. 143-166.
Rizza, A. & Henry, M. Idea di funzione, Actes des journées d’études sur le Rallye mathématique transalpin, vol. 7, Bard (Valle d’Aosta) 2007. Eds. Lucia Grugnetti, François Jaquet, Gianna Bello, Rosanna Fassy, Graziella Telatin, ARMT, 2008, p. 181-198.
Henry, A., Henry M. & Rizza, A. Funzioni per risolvere problemi, La gazzetta di Transalpino, n.1, 2011, http://www.armtint.org/.
Grupo funzione (2013). Il prato di zio Francesco (II). Studio ARMT (http://www.projet-ermitage.org/ARMT/doc/studio-fn6-it.pdf)
(c) ARMT, 2010-2024