La mucca nel frutteto (II)

Identificazione

Rally: 25.I.07 ; categorie: 5, 6 ; ambiti: GM, GP
Famiglie:

• CA - Confrontare aree
• CA/P - Confrontare aree su una quadrettatura
• QUA - Lavorare su una quadrettatura
• QUA/GQ - Gestire poligoni su carta quadrettata

Remarque et suggestion

Sunto

Realizzare su un piano puntato a maglie quadrate due superfici poligonali di uguale perimetro, ma di area crescente. I lati dei poligoni devono essere costituiti dai lati o dalle diagonali delle maglie del piano ed esattamente 8 punti del piano devono essere situati sulla linea poligonale.

Enunciato

Compito per la risoluzione e saperi mobilizzati

- Interpretare il disegno della pianta del frutteto: individuare gli alberi, i pali di diversa lunghezza e i differenti recinti.

- Osservare i contorni dei recinti e riconoscere che ci sono due tipi di pali, quelli la cui lunghezza corrisponde ad un “lato” della maglia quadrata e quelli la cui lunghezza corrisponde ad una “diagonale”. Constatare che ogni contorno dei recinti è composto da quattro pali di ognuno dei due tipi.

- Capire che “pascolare l’erba” nel recinto o “più grande” si riferiscono all’area del recinto, che la forma del recinto può cambiare, ma il perimetro deve restare lo stesso.

- Verificare sui due recinti disegnati che il perimetro sia lo stesso e confrontare le loro aree. Per fare questo, trovare che le aree dei recinti possono esprimersi in quadrati e/o in triangoli (semi quadrati). Per esempio, l’area del recinto di lunedì vale due quadrati interi e 4 triangoli, quella di martedì 3 quadrati interi e 4 triangoli. L’area del recinto di martedì è effettivamente più grande di quella del recinto di lunedì.

Strategie di risoluzione:

- Disegnare a caso un recinto per mercoledì di forma diversa da quella dei primi due, conservarlo se il suo perimetro è uguale a 4 pali lunghi e 4 corti. Determinare la sua area e conservarlo se essa è superiore a quella del recinto di martedì.

- Ricominciare nello stesso modo per il recinto di giovedì.

- Cercare di realizzare un recinto delimitato da 4 pali lunghi e 4 corti. Procedere, in seguito, come prima per confrontare l’area.

- Cercare due recinti di aree più grandi di quella del recinto di martedì con uno dei due metodi precedenti e ordinarli poi a seconda delle loro aree. Quello di area più grande sarà quello per il giovedì, l’altro per il mercoledì.

- Cercare di realizzare un recinto tenendo conto simultaneamente dei due vincoli sul perimetro e sull’area: 4 pali lunghi e 4 corti e all’interno più di 3 quadrati e 4 triangoli o una superficie corrispondente a 5 quadrati o 10 triangoli. Ricominciare fino ad ottenerne uno e poi un secondo, e ordinarli poi secondo le loro aree.

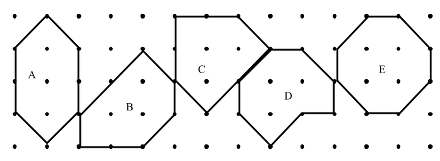
Qualche soluzione per mercoledì (A, B, C, D) e la soluzione per giovedì (E)

- Dare una spiegazione mostrando che c’è un conteggio di quadrati o triangoli o numero di punti interni (secondo il teorema di Pick, l’area in quadrati vale il numero dei punti interni + la metà del numero di punti sul contorno – 1. Gli alunni non possono saperlo, ma l’intuizione “più alberi ci sono all’interno, più grande è l’area” è da accettare come spiegazione).

Risultati

25.I.07

Punteggi attribuiti su 2331 classi di 20 sezioni:

Secondo i criteri dell’analisi a priori:

• 4 punti: Risposta completa (due figure trovate con l’area in progressione e rispetto delle lunghezze dei pali, attribuite correttamente a ognuno dei giorni), con spiegazioni chiare (letterali o disegni con conteggio dei quadrati interi e dei triangoli)
• 3 punti: Risposta completa, ma senza attribuzione dei giorni o senza spiegazione o senza conteggio dei quadrati interi e dei triangoli
• 2 punti: Una sola figura o due figure di stessa area che verifichino le condizioni sulla lunghezza del contorno e sull’area, in progressione rispetto a martedì e al massimo una figura errata che verifichi almeno una delle condizioni sul perimetro o sull’area
• 1 punto: Una o due figure con l’area in progressione, ma che non verificano le condizioni sul perimetro
• 0 punto: Incomprensione del problema

(c) ARMT, 2017-2024