Bien cachés

Identification

Rallye: 21.I.02 ; catégories: 3, 4 ; domaine: GP
Familles:

• IF - Identifier des figures
• IF/INV - Dresser un inventaire

Remarque et suggestion

Résumé

Déterminer le nombre de triangles (12) que l’on peut observer dans une figure composée d’un triangle et de tous les segments dont les extrémités sont les trois sommets et deux autres points choisis sur deux côtés différents.

Enoncé

Tâche de résolution et savoirs mobilisés

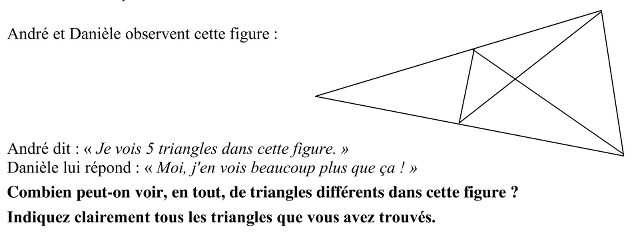
- Après avoir observé que la figure, un grand triangle, se décompose en 5 triangles "élémentaires", prendre en compte la remarque de Danièle et se demander comment elle en voit d’autres: s'il s'agit des 6 déjà mentionnée ou s'il y en a encore d'autres. Observer alors qu’il est possible de voir apparaître des triangles « plus grands », formés de deux, puis trois triangles "élémentaires".

- La tâche est alors de trouver les 4 nouveaux triangles formés de deux triangles "élémentaires", et les 2 triangles formés de trois triangles "élémentaires" qui, avec les 5 triangles "élémentaires" et le triangle complet font 12 = 5 + 4 + 2 + 1.

- La deuxième tâche consiste à « indiquer clairement » les 12 triangles trouvés, en évitant les doublons et sans oublis. Cette tâche est étroitement dépendante de la précédente:

Si les triangles ont été identifiés un à un selon un processus aléatoire, la probabilité qu'ils apparaissent tous n'est pas négligeable parce qu'il n'y a qu'un nombre limité de compositions "nouvelles" (6); mais leur description sera aussi aléatoire.

Si la recherche est organisée de manière consciente et systématique, la description suivra un ordre "logique" et a plus de chances d'être complète, pour autant que les deux types de triangles "nouveaux" soit reconnus ( à deux ou à trois composants):

• soit en reconnaissant les nouveaux triangles selon le nombre de triangles "élémentaires" dont ils sont composés: les 4 triangles de deux composants et les 2 triangles de trois composants (en désignant les cinq triangles élémentaires par une lettre a, b, c, d, e, ou un numéro, ou une couleur, on peut désigner encore plus précisément les 12 triangles. Par exemple: a, b, c, d, e, bc, bd, ce, de, abc, abd, abcde (fig 1);
• soit par des dessins de couleur, en pensant à dessiner plusieurs figures pour que l’inventaire soit « lisible » (l’utilisation de 12 couleurs sur la même figure rend l’inventaire presque « illisible ») (fig 2)
• soit par des les dessins reproduits séparément et ordonnés des 12 triangles.

Notions mathématiques

géométrie, triangle, segment, identification, dénombrement, inventaire, composition

Résultats

21.I.02

Points attribués sur 139 classes de 18 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte (les 12 triangles) avec un inventaire clair et complet (texte ou dessins)
• 3 points: Réponse correcte (12) avec une présentation confuse (par exemple, où il est très difficile de distinguer les différents triangles qui se superposent)
  ou 13 (ou 11) triangles bien présentés mais avec un doublon (ou un oubli)
• 2 points: Réponse avec de 2 à 4 oublis (8 à 10 triangles présentés) sans doublons
  ou réponses avec 1 ou 2 oublis et 1 ou 2 doublons
• 1 point: Réponse ne faisant apparaître que 6 à 7 triangles
• 0 point: Incompréhension du problème
  ou moins de 6 triangles
  ou réponses avec d’autre polygones non triangles

La réussite est "moyenne" avec une progression qui semble significative de la cat 3 à la catégorie 4. Il y a peu "d’incompréhension du problème".

Procédures, obstacles et erreurs relevés

L'examen d'une quarantaine de copies permet de constater que l'obstacle essentiel du problème réside dans l'organisation de l'inventaire.

Dans la majorité des cas, les triangles "composés" sont identifiés, en particulier les assemblages de deux des cinq triangles "élémentaires", adjacents. Les compositions de trois triangles apparaissent un peu moins souvent. On ne relève que de rares réponses "cinq triangles" ou "six triangles" (les cinq triangles "élémentaires" et la figure complète, "le grand"). C'est au moment de dresser l'inventaire qu'apparaissent les difficultés.

• La procédure la plus fréquente est de marquer de couleurs différentes les périmètres des triangles. Ces coloriages sont cependant effectués sans qu'on puisse y percevoir un ordre ou un choix conscient au delà des triangles "élémentaires. On entoure par exemple les deux triangles de droite en bas (e et d) par un trait qui se superpose aux couleurs périmètres déjà coloriés, puis on en choisit deux autres et d'autres encore, mais la superposition des traits de couleur empêche alors l'identification de tous assemblages et on arrive ainsi souvent à des réponses "10 triangles" ou "11 triangles".
• La procédure de coloriage des superficies des triangles, plus rare, ne permet pas d'aller au-delà d'une superposition.
• Les dessins séparés de tous les triangles identifiés, au-dessous de la figure de départ, sont assez fréquent mais se heurtent à la difficulté de la construction géométrique. Les triangles reportés ne sont pas vraiment reconnaissables et par conséquent cette procédure aboutit à des inventaires incomplets.
• Dans plusieurs cas, les triangles sont notés par les premiers nombres naturels: 1, 2, 3, 4, 5 au centre de chacun des triangles "élémentaires" puis 6, 7, 8 ... notés sur des côtés communs à deux triangles. Cette procédure permet d'arriver en général à la réponse "10 triangles" car elle ignore les assemblages de trois triangles.
• On note encore des regroupements de deux triangles par un trait (un arc) passant au-dessus de leur frontière commune et des regroupements de trois triangles par un arc qui les relie.

Dans les copies examinées, on ne relève aucun inventaire à partir d'une désignation des cinq triangles "élémentaires" (par des numéros, des couleurs ou des lettres). Le seul inventaire qui paraît organisé apparaît dans trois des copies examinées à partir de regroupement par nombres de triangles:

Exemple

• 1 triangle : 5
• 2 triangles : 4
• 3 triangles : 2
• 5 triangles : 1
• avec les pourtours dessinés sur la figure en rouge pour les "2 triangles" et en bleu pour les "3 triangles.

L'erreur la plus fréquente est "10 triangles", résultant de l'oubli des 2 triangles composés de trois triangles "élémentaires".

Exploitations didactiques

Variantes : Il y a de nombreux autres problèmes du RMT sur les triangles à identifier Des triangles, oui, mais combien? (21.I.11), Combien de triangles? (07.F.12) Le foulard de Grand-mère (13.I.05), Les triangles (I) (16.I.04 et d’autres encore.

Le problème Le foulard de Grand-mère (13.I.05), absolument comparable à celui-ci, mais avec 17 triangles à découvrir au lieu de 12 et avec 8 triangles de base au lieu de 5 donnait des moyenne de 1,7 et 2,2 pour les catégories 3 et 4, du même ordre de grandeur que celles de ce problème Bien cachés (21.I.02).

(c) ARMT, 2013-2024