Des triangles sur une planche à clous

Identification

Rallye: 27.I.18 ; catégories: 8, 9, 10 ; domaines: GP, GM
Familles:

• CA - Comparer des aires
• CA/P - Comparer des aires sur un quadrillage
• LA - Utiliser des mesures de longueurs et aires
• LG - Déterminer un lieu géométrique
• QUA - Travailler sur un quadrillage
• QUA/GQ - Traiter des polygones sur quadrillages

Remarque et suggestion

Résumé

Un triangle est déterminé par trois sommets se situant sur les intersections d’un réseau de points à maille carrée (planche à clous), aucun de ses côtés n’est situé sur une ligne du réseau. Trouver tous les autres triangles de même aire dont deux sommets donnés sont inchangés et le troisième sommet est un autre point du réseau.

Enoncé

Tâche de résolution et savoirs mobilisés

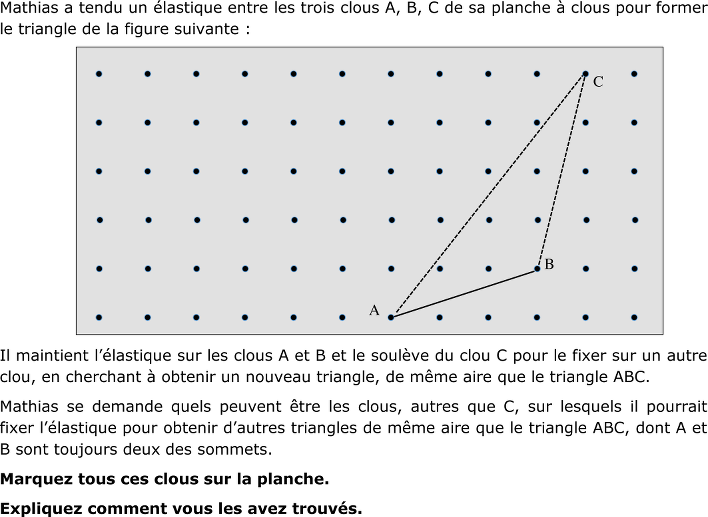
Analyse a priori:

- Observer la figure et comprendre qu’il faudra tenir compte des limites de la planche à clous, de la disposition des clous sur la planche et de l’élastique tendu entre trois clous, de la position de deux des sommets qui est contrainte et de l’aire qui doit rester la même.

- Mettre en œuvre la formule de l’aire du triangle comme moitié du produit des mesures d’une base et de la hauteur correspondante (b h / 2) et, par un raisonnement déductif, aboutir au constat que si la mesure d’un côté (b) et l’aire (A) sont constantes, la hauteur (h) doit aussi être constante.

- Identifier la « hauteur » [CH] qui est portée par la perpendiculaire à la droite qui porte la base [AB] et prendre conscience que le point H, intersection des deux droites, n’est pas sur la base mais sur son prolongement.

- Identifier les emplacements où pourraient se situer les sommets différents de C lorsque l’autre extrémité H se déplace sur la droite (AB). Ce lieu géométrique est celui de l’extrémité du « segment hauteur », de mesure constante, c’est la droite parallèle à la base passant par C).

- Les trois constats précédents conduisent à l’identification des trois autres clous distincts de C situés sur la droite parallèle à (AB) passant par C.

Ou

- Après avoir déduit que la hauteur du triangle correspondant au côté [AB] doit être constante, tracer et mesurer la hauteur [CH], puis tracer la perpendiculaire à la droite (AB) passant par un autre point de la grille et sur cette droite mesurer la distance du point à la droite (AB). Si cette mesure est égale à la longueur CH, le point convient, sinon recommencer avec d’autres points.

Ou

- Déterminer l’aire du triangle ABC et chercher d’autres triangles de même aire, dont deux sommets sont A et B. Il y a plusieurs manières de déterminer l’aire, en particulier :

- L’aire, 5,5 carrés de la grille est déterminée par « pavage » (à partir de figures d’aires facilement déterminées : rectangle circonscrit, triangles rectangles), par décomposition et « soustractions» (un exemple est donné par la figure ci-dessous). La procédure longue et fastidieuse consiste alors à tester d’autres positions du troisième sommet sur la grille et à déterminer par pavages l’aire du triangle ainsi déterminé. L’essai de déplacer le sommet C de 1 carreau vers la gauche aboutirait à une aire de 6 ; en descendant ensuite de 1 carreau vers le bas, on arriverait à 5, etc.).

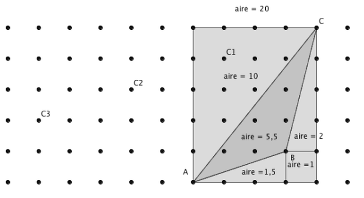
- Ou déterminer approximativement l’aire (par comptage des carrés entiers et recollage de parties de carrés ou utilisation de la formule de l’aire d’un triangle à partir de mesures, en cm, prises sur la figure).

Remarque : L’aire peut être calculée par la formule de Pick (vu qu’il y a un quadrillage qui est une planche à clous). A = p/2 + i – 1 = 3/2 + 5 – 1 = 5,5 (p désigne le nombre de points sur les côtés du polygone et i le nombre de points à l’intérieur du polygone).

Notions mathématiques

triangle, sommet, base, hauteur, inventaire, quadrillage, perpendiculaire, aire. équivalence, lieu géométrique, formule

Résultats

27.I.18

Points attribués sur 1254 classes de 20 sections:

Selon les critères déterminés lors de l’analyse a priori :

• 4 points: Réponse correcte avec les trois points (clous) C1, C2 et C3 (sans points incorrects) et explications claires (procédure par la parallèle ou hauteur constante ou calcul des trois aires, …)
• 3 points: Réponse correcte avec les trois points (clous) C1, C2 et C3 (sans points incorrects), sans explications
  ou oubli d’une ou de deux des positions, mais avec une démarche correcte bien expliquée (voir explication précédente)
  ou 4 points « C » donnés dont 3 corrects et une 4e position erronée due à des calculs pas suffisamment précis
• 2 points: Une ou deux positions trouvées mais sans explication
  ou calcul correct de l’aire du triangle ABC et au moins une tentative décrite de recherche d’autres positions possibles de « C » avec des calculs d’aires détaillés
• 1 point: Calcul de l’aire du triangle ABC à partir de mesurages
  ou tentative de détermination de l’aire du triangle ABC par pavage sans arriver au résultat correct
  ou d’autres débuts cohérents de recherche (par exemple affirmation que les triangles ayant tous la même base [AB] et la même aire, ils doivent avoir la même hauteur)
  ou dessin du triangle symétrique du triangle ABC par rapport à l’axe du côté [AB], ce triangle ayant la même aire que ABC, mais le troisième sommet n'est pas sur un clou
• 0 point: Incompréhension du problème

Procédures, obstacles et erreurs relevés

Procédures

Sur les 511 copies examinées en catégorie 8 et 244 copies en catégories 9 et 10, des sections de Bourg en Bresse (BB) et Franche-Comté (FC) en France, de Cagliari (CA), de Parme (PR), de Puglia (PU), de Rozzano (RZ), de Siena (SI), de Sassari (SS) en Italie, seule une partie des classes a trouvé au moins un clou en suivant une procédure et un raisonnement corrects.

L'analyse a posteriori des copies a montré que les procédures prévues dans l'analyse a priori étaient mises en œuvre par ceux qui avaient correctement résolu le problème.

Dans l'ensemble, la plupart des élèves ont compris la tâche mathématique, celle de construire avec un fil élastique d'autres triangles équivalents à celui donné ; cependant, dans la recherche de triangles de mêmes aires, plusieurs erreurs émergent en raison d'idées fausses liées au calcul de l'aire (formule incorrecte) et au concept de hauteur d'un triangle, comme l’ont souligné, en particulier, Brunella Brogi et Gloria Giacomelli, qui disent que même lorsque la formule de l'aire est correcte, la mesure de la hauteur est prise sur un segment qui est dessiné en position verticale, passant par le sommet C, mais non perpendiculaire à la base (AB), la mesure de cette "hauteur" est exprimée soit en cm soit en nombre de clous. L'idée fausse selon laquelle le « pied » de la hauteur est toujours au milieu de la base est également apparue. Dans d'autres cas, les élèves ont mis en œuvre des procédures non prévues et dans certains cas, inadaptées pour résoudre le problème.

On relève une différence "cognitive" entre les procédures suivies par les groupes d’élèves :

- ceux qui résolvent le problème en utilisant une procédure proche de celles prévues par l'analyse a priori, soit avec mesure de la hauteur relative à (AB), calcul de l'aire du triangle et tracé de la droite parallèle à (AB) passant par C, dans une démarche déjà bien structurée, soit avec une procédure qui met en jeu la hauteur relative au côté [AB] et son déplacement par translation ;

- ceux qui confondent encore l'aire et le périmètre ;

- ceux qui calculent l'aire d'un triangle en effectuant le demi produit des mesures de deux des côtés.

Parmi ces "extrêmes", en plus des groupes mentionnés qui ont trouvé au moins un clou correct en utilisant une procédure correcte, il y a eu plusieurs groupes qui n’y sont pas parvenus. Néanmoins certains d’entre eux se sont en partie approprié le problème, sans cependant, se rendre compte qu’utiliser par exemple la découpe du triangle donné ou que dessiner une sorte de symétrie axiale ne satisfaisait pas aux deux contraintes posées par le problème : même base et troisième sommet sur un clou. Dans certains cas, les élèves n’ont pas assimilé toutes les conditions posées par le problème et ont proposé en réponse des figures fausses, car ils les ont par exemple obtenues en soulevant l'élastique de tous les sommets et pas seulement du point C, ou parce qu'ils n’ont pas compris que la planche à clous sur laquelle on leur demandait d’identifier les triangles de même aire correspondait à celle présentée sur le dessin.

Obstacles et erreurs

Le problème en question a permis de mettre en évidence des obstacles et des erreurs concernant les connaissances et les savoir-faire autour de concepts qui devraient être acquis par des élèves des catégories 8, 9 et 10.

Les principaux obstacles mis en évidence sont les suivants :

1. Difficulté à identifier la hauteur relative au côté [AB]. Les élèves n’ont pas réalisé que H, le pied de la hauteur, intersection de deux droites (base et hauteur), n’appartient pas au côté, mais à la droite qui le porte. En fait, la définition de la hauteur comme : « segment issu d’un sommet et qui est perpendiculaire au côté opposé à ce sommet » pourrait amener les élèves à considérer que la hauteur doit nécessairement « tomber » sur le côté.

2. Difficulté à identifier les positions possibles des sommets pour lesquelles l’aire du triangle de base [AB] reste constante ; ces points constituent le lieu géométrique de l’ensemble des points (sur le dessin fourni) situés à une distance donnée de la droite (AB) et qui se trouvent sur une parallèle à cette base.

3. La non appropriation du concept de hauteur souvent identifiée par les élèves à l'un des côtés du triangle.

4. La difficulté à tracer la hauteur, surtout lorsque les figures géométriques ne sont pas en position prototypique et si de plus le pied de la hauteur n’appartient pas au côté mais à la droite qui le porte.

Les principales erreurs qui sont apparues sont les suivantes :

1. Dans le calcul de l’aire :

a. calcul du demi-produit des mesures de deux des côtés du triangle ;

b. calcul du demi-produit 4 x 5 /2 correspondant aux mesures des côtés du triangle rectangle dont l’hypoténuse est AC et les côtés sont horizontaux et verticaux;

c. calcul du demi-produit de la base par la hauteur avec mesure incorrecte de cette dernière.

2. Dessin d'une « sorte » de triangle ABC1 symétrique du triangle ABC en cherchant à faire coïncider le sommet C1 avec l'un des clous.

3. Mauvaise application de la formule de Pick : des élèves ont considéré comme étant équivalents des triangles qui avaient le même nombre de clous internes ou le même nombre de clous externes.

Exploitations didactiques

Ce problème, comme d'autres du RMT, a clairement mis en évidence les difficultés rencontrées par les élèves concernant les hauteurs des figures géométriques dont les côtés ne sont ni horizontaux et ni verticaux (souvent peu présentes dans les manuels scolaires, voire pas du tout) ou en présence de triangles possédant un angle obtus, ou encore face à la définition de la hauteur comme étant « une droite qui passe par un sommet et qui est perpendiculaire au côté opposé à ce sommet ».

À partir de ces constats résultant de l'analyse a posteriori de ce problème, il pourrait être utile de :

1. Privilégier la définition de la hauteur d'un triangle en tant que : distance entre un côté, choisi comme base, et son sommet opposé.

2. Différencier hauteur en tant que segment ou droite et hauteur en tant que mesure.

3. Combattre l'idée fausse selon laquelle la hauteur est liée à la verticalité.

4. Présenter des figures géométriques dans une orientation différente de l'horizontale et de la verticale (B. Brogi, 2019).

5. Combattre l'idée fausse selon laquelle le pied de la hauteur est toujours au milieu de la base.

6. Identifier les hauteurs sur les figures où le pied de la hauteur est sur la droite à laquelle la base appartient.

7. Développer le concept de lieu géométrique de l'extrémité du segment hauteur (de mesure constante) lorsqu'il se déplace par translation dans la direction de sa base. Cela permettra d'acquérir que les triangles qui ont la même base et la même hauteur ont la même aire.

8. Proposer des problèmes dans lesquels la hauteur est à déterminer, par exemple tirés de la banque de problèmes ARMT.

9. Concevoir des parcours d'apprentissage en utilisant des problèmes tirés de la banque ARMT, en limitant l'utilisation d'exercices répétitifs pour calculer les surfaces dans les manuels.

Le problème Découpage de triangles (19.II.13 cat. 6,7,8) peut aider les élèves à se libérer du dessin des triangles dans une position prototypique. La résolution de ce problème conduira à l'observation de ce que Raymond Duval (pré-impression, 2020) a appelé "unités figurales 1D", ce qui permettra d'identifier les côtés de longueur égale du triangle isocèle comme la diagonale du rectangle 4 x 2. Un problème tel que "Découpages de triangles" permet de mettre en évidence des obstacles caractéristiques sur des notions qui sembleraient avoir été acquises, comme le triangle isocèle, sa position et l’égalité des mesures des côtés. Il est clairement observé que l'image du triangle isocèle que les élèves ont, est celle d'une figure à trois côtés, dont l'un est horizontal et les deux autres, de mesures égales, sont obliques. Il s'agit d'une figure symétrique à axe vertical (au sens de Lismont & Rouche, 2001), où l'objet de référence est le toit (ex. Marchini et al., 2002). Le terme base signifie que ce côté est non seulement horizontal mais aussi en bas. Le modèle du drapeau, (toujours dans Marchini et al. susmentionné), est beaucoup moins fréquent.

Dans la banque de problèmes, plusieurs problèmes permettent de confronter les élèves aux difficultés évoquées ci-dessus. Entre autres :

Il Le manteau de Martin (17.F.14 cat. 7, 8, 9, 10); MadamePapillon (25.II.16 cat. 8, 9, 10) ; Le potager I ( 26.II.12 cat. 6, 7, 8)

Bibliographie

Brogi, B. : 2019, Matematica in classe con il Rally Matematico Transalpino, “un’insegnante racconta”/Mathématiques en classe avec le Rallye Mathématique Transalpin, « le témoignage d’une enseignante’, Gazette. 9, 117-123.

Duval, R. : preprint, Le premier seuil dans l’apprentissage de la géométrie : VOIR les Figures / Il primo passo nell’apprendimento: “VEDERE” le figure, Gazette di Transalpin n. 10 (sera vaccessible sur le site de l’ARMT courant 2020).

Lismont, L, Rouche, N. (a cura di) : 2001, Forme et mouvements, CREM.

Marchini C., Rinaldi M.G., Bedulli M., Grugnetti L .: 2002, Tetti e bandiere, Processi didattici innovativi per la Matematica nella scuola dell'obbligo, Pitagora (Bo), 223-236.

(c) ARMT, 2019-2024